|
续杯之前的补充: 说明一下,前两篇的研读分享并不是说只看这两篇文章就可以了,拿出来的如果真耐心看完原论文肯定有更加深刻的理解,这里分享的目的是方便大家学习,论文有利有弊,理论上的天马行空,实际工况上可能并不一定适用,大家要彻底理解后做取舍。 另外,关于不同工况下对IGBT基板散热的处理也不一样,这里分析的是汽车厂常用的带PinFin独特结构的IGBT模块,第一篇就提到了有的工业场合在功率不大的情况下,因为可以在额定工况运行达到热平衡,所以不会超过截止保护温度,所以在不要求精确反馈实时温度的条件下大概率公司也不会浪费算力做此功能。论文中有提到,在以冷却液进行冷却时有些结论还是很有参考意义的,这里提一下。 如下图1图2可知: 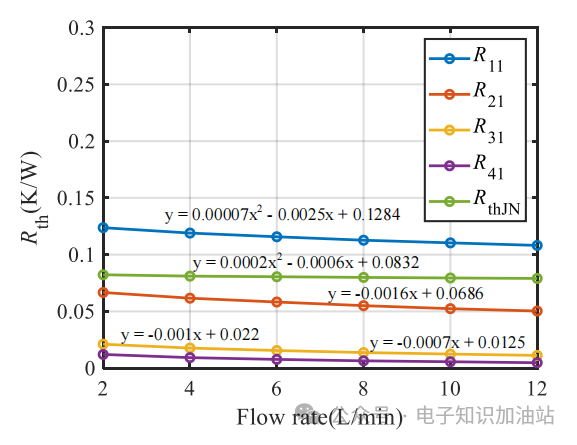 图1 不同冷却液流速下稳态热阻参数的变化  图2 不同冷却液温度下稳态热阻参数的变化 结论: 冷却液流速对基板以下或者称之为散热器部分的热阻抗有一定的影响,水温则对系统热阻抗几乎没有影响。 有了上面的结论,我们至少可以摒弃一些关于冷却液会造成影响的顾虑,至于论文中提到的上管根据NTC来做结温,下管根据无水温传感器预估水温后再做下管估算的优化方案,这里不再多做介绍。 补充完毕~  公式推导: 如图:  图3 等效热容热阻的Foster热网络模型图示 等效图不再多做介绍。只写出一阶而不是四阶传递函数。在不考虑芯片耗散热量在水平方向扩散的前提下,IGBT模块的等效散热形式可以用一维热网络来近似,其中图3就是一维局部热路模型。其他三个一摸一样,结果累加就是了。 如上图,两端温差Ti 相当于电压U,而P损耗相当于电流I,对于热阻R来说还是相当于R,那么有公式: 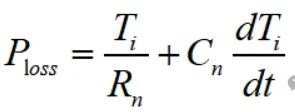 ------公式1 由公式1可以进行拉普拉斯变换为: 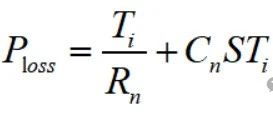 ------公式2 公式2变一下型可得: 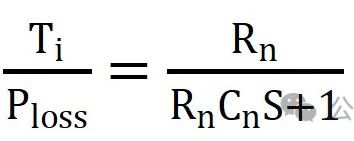 ------公式3 多嘴部分: ========================================= 前面公式1~3推导下来比较简单,有点儿电路基础的一眼看过来就知道,不过一个电阻电容串联,如下图: 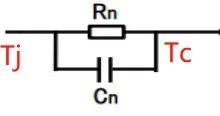 4 一阶等效热网络模型图示 那就可以直接写出传递函数: 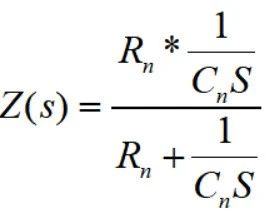 ------公式4 公式4化简后的结果就是公式3的右半部分。 =========================================== 接着说: 由公式3的拉普拉斯变换,再转到时域,可以得到公式: 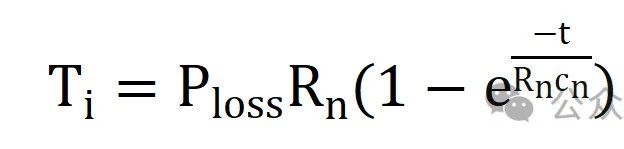 ------公式5 刚才有提到,这只是一阶的,还有三阶呢,那就累加起来得到总温差: 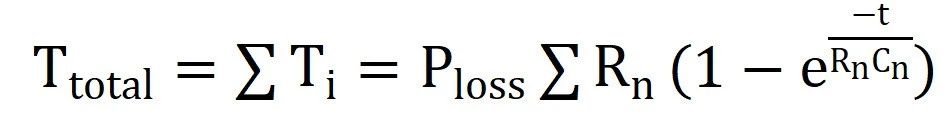 ------公式6 到这里基本上已经结束了,求出了总的温差,再加上参考温度,就可以得到结温最终值了。但结合手册给出的热阻抗曲线,我们也要得到这样一条曲线,所以,公式6再变下型,可得:  ------公式7 式中Zth表示热阻抗,n表示希望拟合的Foster网络阶数,Rn(n=1、2、3、4)为拟合出的每阶等效热阻,热时间常数τn为拟合的等效热阻Rn与热容Cn的积。 到这里才正儿八经的把我们要求的热阻抗曲线给求出来,就是公式7。 那么怎么建模呢? 这个时候需要进行公式离散化,由公式3得到差分方程,先进行Z变换: 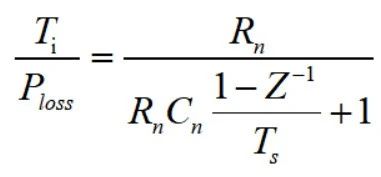 ------公式8 对公式8展开:  ------公式9 由公式9可以定义两个系数: 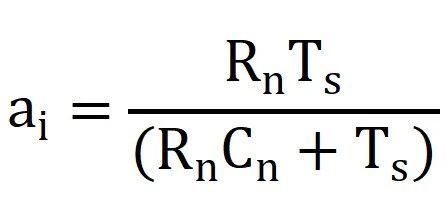 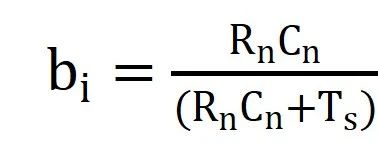 建模使用到的公式为:  ------公式10 |





