LC滤波器是Buck电源及类似电源拓扑的输出环节,本小节单独分析一下LC滤波器的性能,以更方便理解Buck电路的特性。1、 理想的LC滤波器的基本频域分析当我们考虑一个理想的 LC 低通滤波器时,我们可以使用基本的电路分析来推导其传递函数。LC 低通滤波器由一个电感(L)和一个电容(C)组成,如图11.30所示。 图 11.30 理想的LC低通滤波器电路 传递函数表示输入和输出之间的关系。对于LC低通滤波器,我们可以使用基本的电路元件方程来得到传递函数。假设输入为电压Vin,输出为电压Vout。 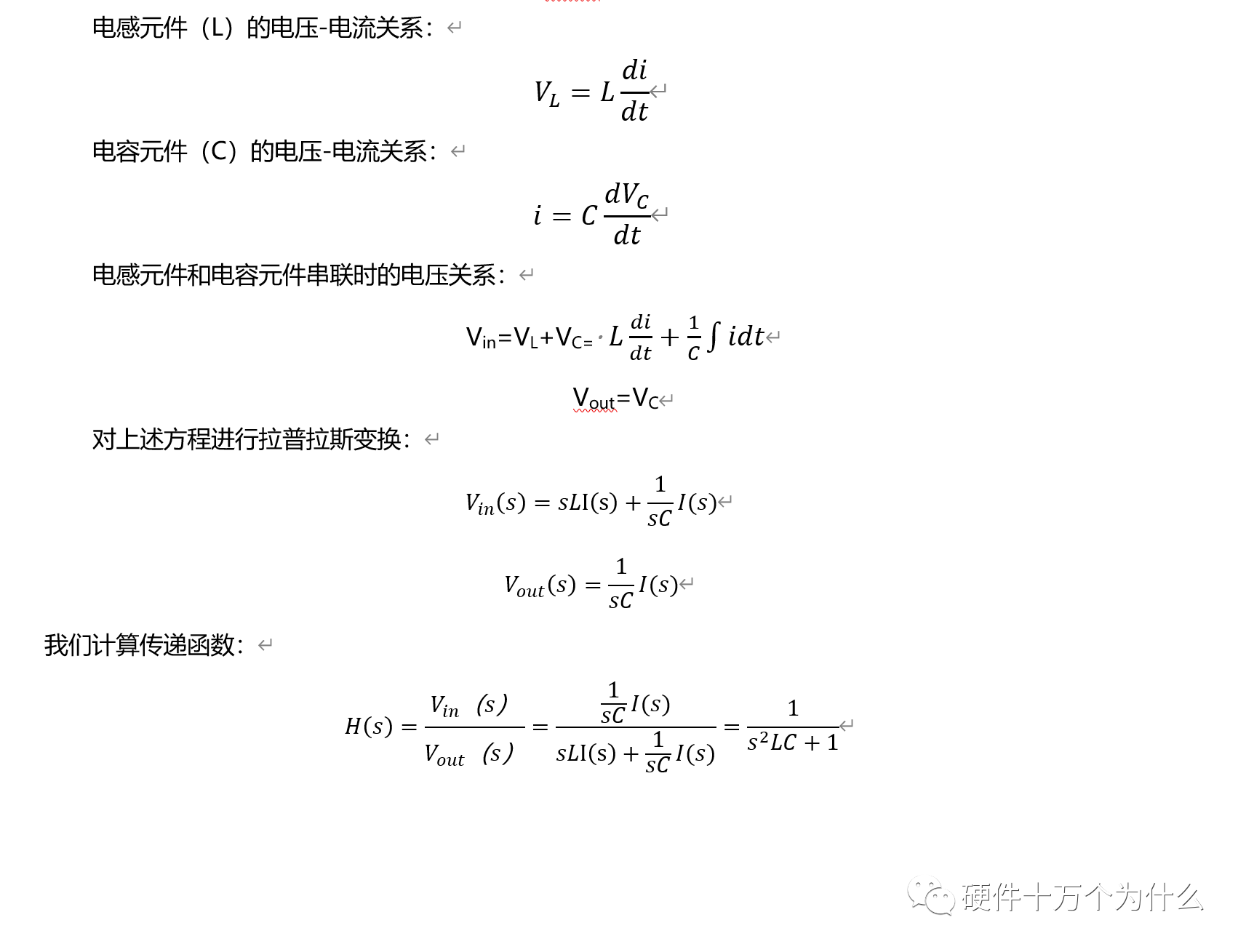 理想状态下,传递函数有一个双极点,波特图如图11.31所示。 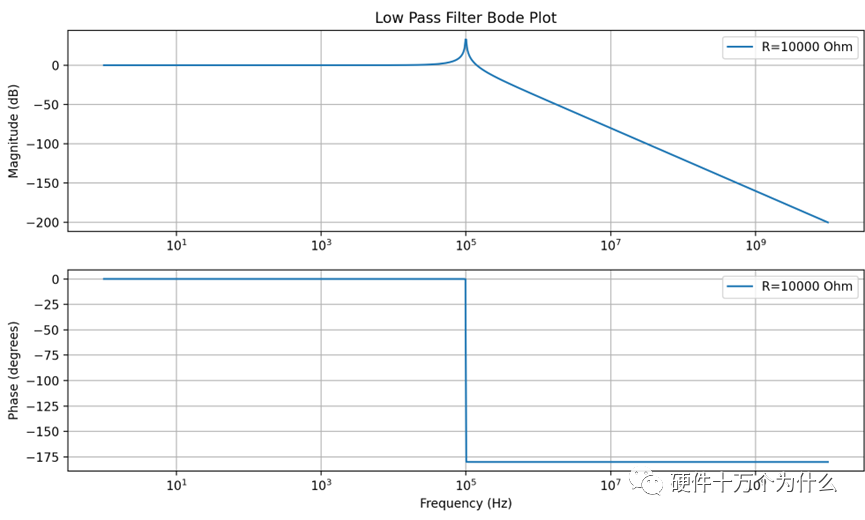 图 11.31 理想的LC低通滤波器波特图 当我们考虑电容并联一个电阻,跟开关电源的输出电容与负载并联一个电路结构,电路如图11.32所示。我们会发现,当考虑这个负载之后,我们会改变传递函数的零极点。 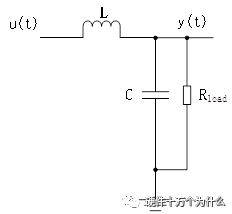 图 11.32 考虑负载的LC低通滤波器电路图 此时需要先将电容与负载电阻进行并联,然后再跟L进行分压。此时传递函数为:  此时我们会发现两个极点不重合了。传递函数受到了负载阻抗的影响,从波特图上,我们也可以看到三个负载值不同形成了不同的波特图的形态,如图11.33所示。 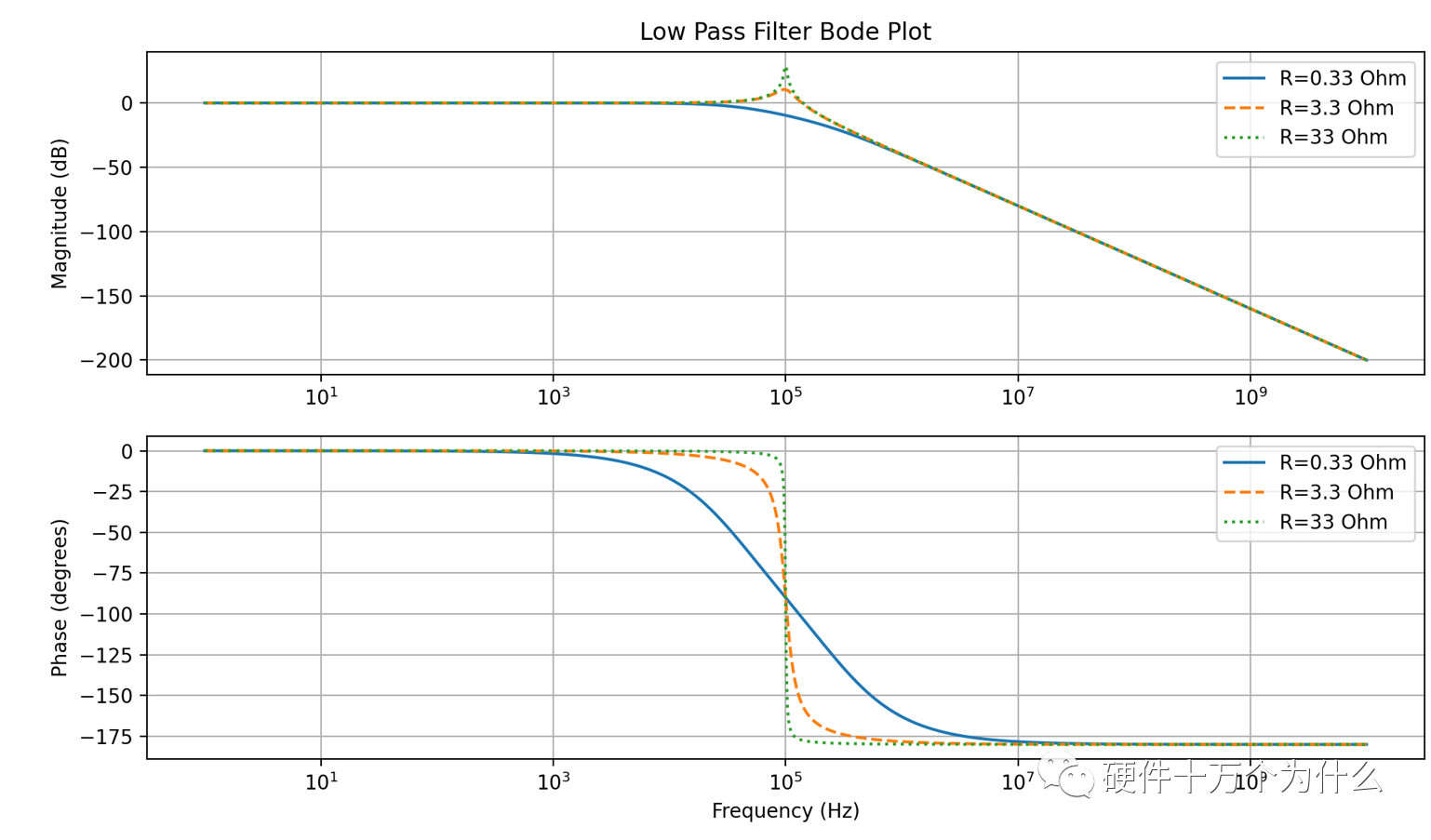 图 11.33 考虑负载的LC低通滤波器波特图 LC滤波器的典型原理图如图11.34所示,此处的RLOAD用来作为电路的输出负载电阻。RDCR为电感的寄生串联电阻,RESR为输出电容的寄生串联电阻(或者称之为ESR),这些寄生参数对于电路的某些频域性能有很大的影响,所以不能忽略。 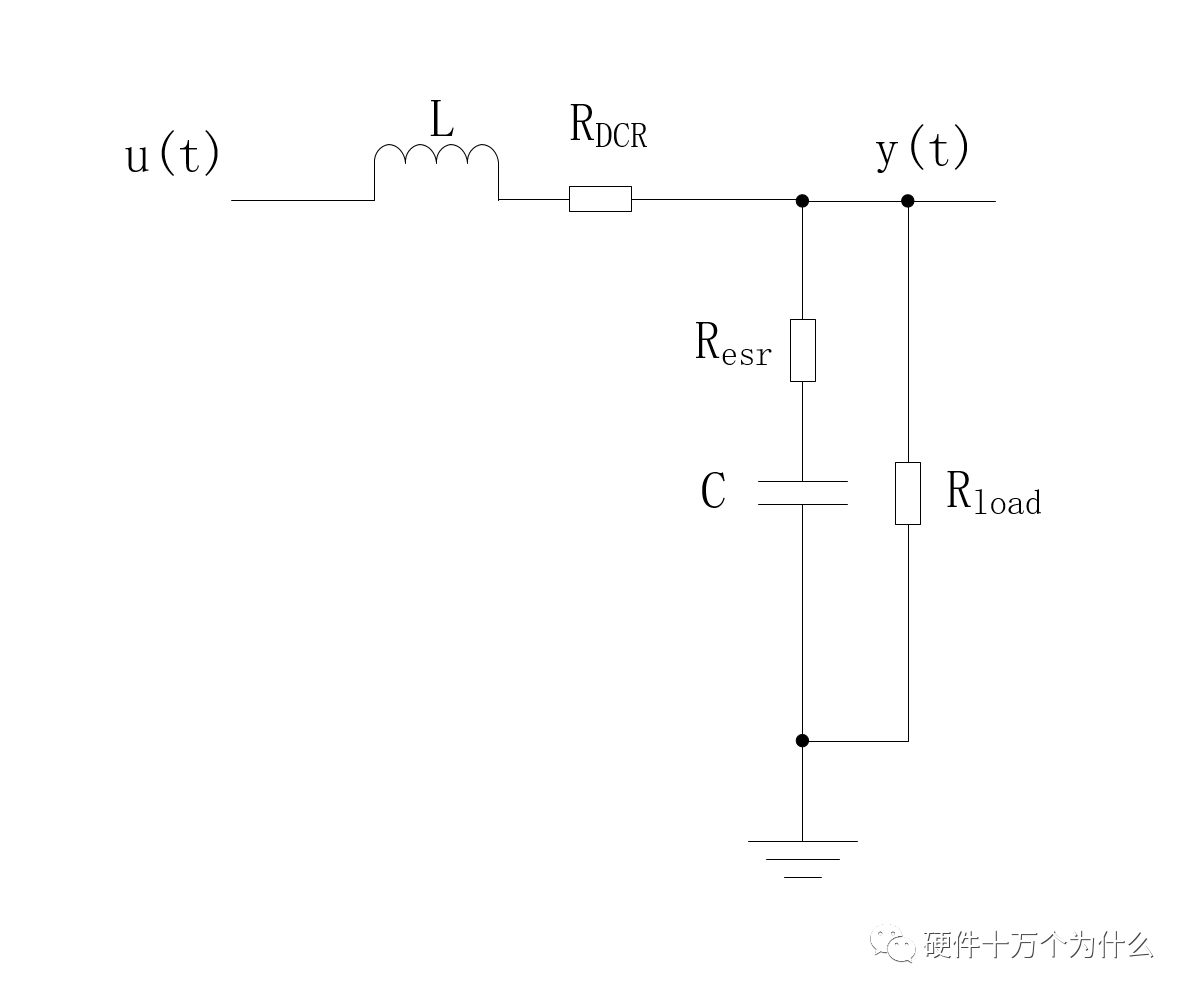 图 11.34 典型LC滤波器的原理图 这个网络输入端电压为Vin,输出端电压为Vout,根据电路分压的基本原理,我们可以推导出电路的传递函数。   上面这个传递函数经过推导整理后,可以得到更为标准的传递函数,可以看出分子上RESR和C形成一个零点 ,分母上LC构成双极点。 实际模型的 LC滤波器的传递函数与波特图对于LC滤波器,我们设定RDCR=29mΩ,Resr=40mΩ,C=100uF,L=10uF。我们除了定义L、C及其寄生电阻之外,还定义了负载电阻,并且定义了三种不同的负载电阻,方便我们分析负载电阻的不同影响,三个负载:Rload1=0.33Ω,Rload2=0.33Ω,,Rload3=33Ω。这里负载电阻越大,则相应的负载电流越小。同时,大家可以这么理解,并联大电阻相当于串联小电阻,而串联的电阻小时,对LC系统的阻尼更小。负载电阻对二阶系统的转折频率没有影响,但是对波形的极点的幅值影响很大,如图11.35所示。 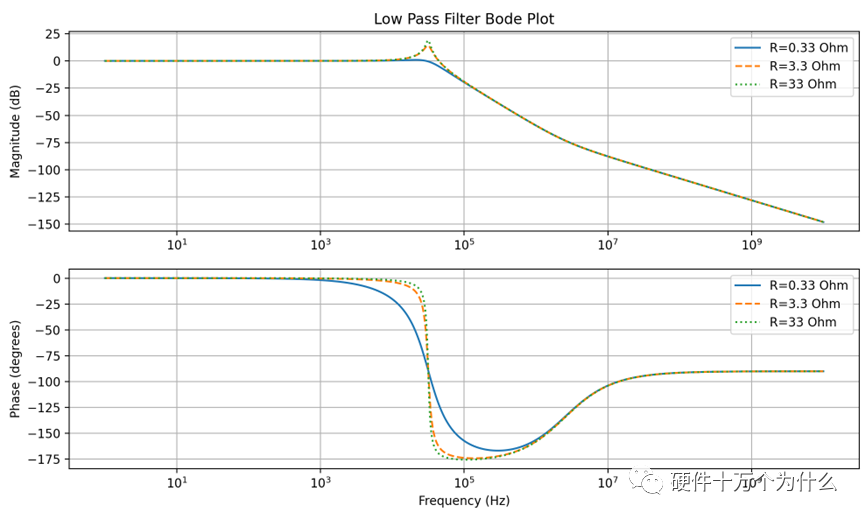 图 11.35 不同条件的LC滤波器波特图 这里可以得出一个重要结论,就是LC寄生电阻参数越小,则对应极点的幅值越大,如图11.35中的点状线曲线,其增益谐振峰值远高于另外两条曲线。 同时,我们观察相位曲线变化,图11.35中对应高Q值 的点状曲线下降最陡峭,LC寄生电阻足够小的时候,可以看到相位下掉速度会更快,所以寄生参数对于减缓相位下掉是有帮 助的。 为了完成以上内容,用python写了一段代码。代码主体是ChatGPT帮我写的,但是ChatGPT对电路和理解和公式推导还是基本100%有错误,需要手动修正一下。以下代码贴出来,供参考。 基本上,用ChatGPT+Python能够完成很多波形图的绘制了。前提是你自己搞得懂基本原理,并且清楚正确答案是什么。   |





