压缩技术的讨论EDT与大规模数据压缩EDT(Embedded Deterministic Test)是专为应对大规模测量数据体积增长所提出的压缩逻辑方案。在本篇文章中,我们将从物理学和电路工程的视角深入探讨其中的核心组件——LFSR(线性反馈移位寄存器)。 (P.s.,最近突然新增许多关注和分享,原意是在未成规模之前,朋友群里小范围分享。当下不希望有暴涨的关注,会带来一定的压力。请在目标实现之前,观众们减少分享,谢谢。) 前言: 数据压缩是什么? 简言之,数据压缩意味着在不丢失原始信息的基础上,通过新的表述方式来表示数据,这样可以更节省存储空间。想象一下,如果我们使用数据压缩的技术去评估ATPG向量,其压缩的上限又会是多少呢? 香农熵或信息熵在信息论中代表系统的不确定性。基于这一概念,我们可以得知一条信息的预期值。例如,ATPG工具生成一个模式时,它会针对一组故障,而结果中只有少数扫描触发器需赋特定值。对于这种多条链条组成的信息流,如果我们将其视为一个二维寄存器系统,那其中的大多数值实际上都是冗余的。 以一个实际例子为例:考虑一个由100条、每条长500的CHAIN组成的矩阵。大部分值我们都视为0。如果这个矩阵中有49020个0,其信息熵是多少呢?经过计算, 总信息量=n0×I(0)+n非0×I(非0),I(xi)=−log2p(xi) 这个矩阵的平均信息量为6959.44比特,即描述这个信息至少需要6960比特。压缩率高达86.08%。 然而,真实的压缩效果远远超过这个比例,为什么呢? 为何信息熵的压缩效果并不是最优的? ATPG测试的主要目的不是无损数据压缩,更重要的是如何产生伪随机序列。实际上,EDT允许有损压缩。通过LFSR用于产生伪随机测试模式,LBIST模式下还有MISR(多输入签名寄存器)则用于收集和压缩响应。在此过程中,并不需要对数据本身进行深入的统计分析,只需保证数据足够随机,就能在fault等价理论上实现高覆盖概率测试。 那么,关键在于如何产生这种随机测试向量。答案就是:LFSR。 RING LFSR RING LFSR是对传统LFSR概念的进一步发展,它在实现上对寄存器进行了优化,更注重短传播路径和小fanout。但其核心仍是LFSR。接下来,我们将展示一个LFSR的示意图,其中,图a的右侧寄存器经模2加工后,与下一级的左侧寄存器一同形成了线性反馈。 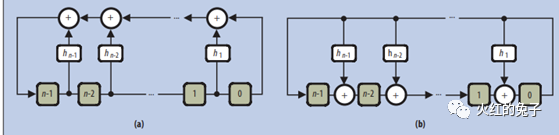 等价的多项式公式为: 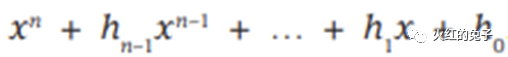 这个多项式看起来很眼熟,你是否觉得它与PRBS(Pseudo-Random Binary Sequence)的公式极为相似?没错,使用最大多项式,我们确实可以描述2^n-1 的数值范围。 那么,图中的a和图b有何不同呢? 在图a中,从最右侧到最左侧的XOR级数较多,这可能导致时序延迟。而图b虽然降低了时序影响,但最右侧的负载过大,这也是个问题。 这时,Ring LFSR(环形线性反馈移位寄存器)进入了我们的视野。它是对传统LFSR的优化版本。与其他几种LFSR相比,RING LFSR在IC实现策略上堪称全能的五边形战士! 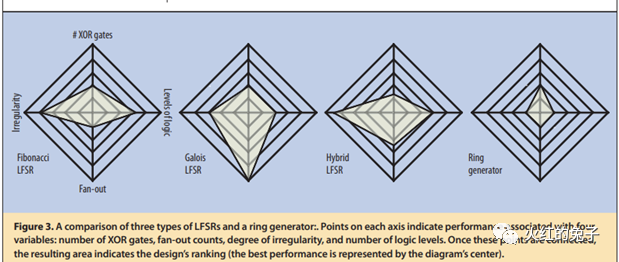 经过计算,一个RING LFSR的例子如下图所示: 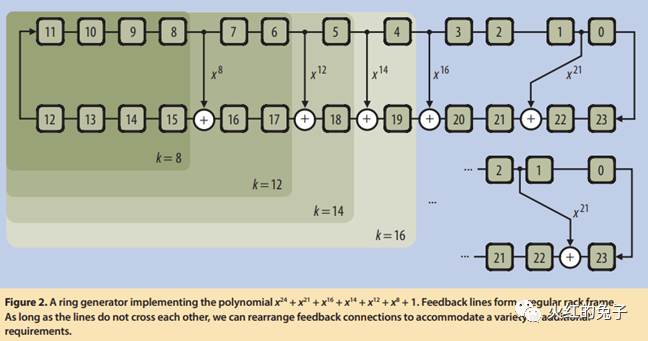 上面的这个RING LFSR的多项式经过特定设计,可以产生一个长达2^24−1 的伪随机二进制序列,之后随时钟脉冲会重复。这样的长序列在许多应用中是很有价值的,例如在数字通信、密码学和硬件测试中。其等价的多项式为: x^24+x^21+x^16+x^14+x^12+x^8+1 来观察一下有什么差别,想一下我们正常的泰勒展开?思考泰勒展开。它是一个将函数表示为无穷级数的方式,通常包含所有幂次方。但是,当我们看到某个特定的多项式,我们可能会发现它并不包括所有的幂次方。这是否意味着这个多项式不完整或者有误?其实不然。这涉及到一个叫做“完备多项式集合”的概念。在这个上下文中,“完备”并不意味着必须包括所有幂次方。相反,它指的是这样一个多项式集合,只要其中的多项式能够代表一个特定范围内的所有值,这个范围就是2^n−1。 不同于泰勒展开,一个完备的多项式不必包含所有的幂次方。关键在于它能否准确地表达一个给定的值范围。RING GENERATOR的实现目的就是这样的完备的多项式。如下图例子所示,两个同幂的多项式表达的值范围并不相同: 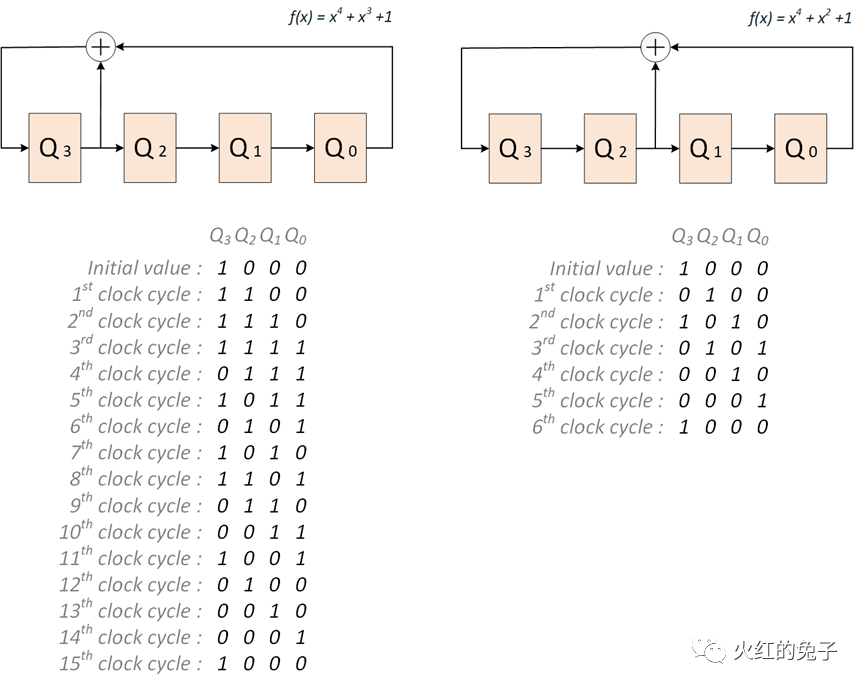 因此,请记住,LFSR的一个关键特点是,给定的多项式和一个非零的初始状态,它会产生一个伪随机序列,但这个序列是可以预测的,因为它总是以相同的方式重复。我们在随机种子确定之后,对于预期的数据仿真可以参考一下如下4比特的LFSR序列。 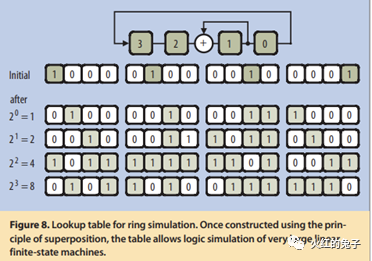 如果大家对矩阵比较了解的话,会发现矩阵的表达和计算是最清晰的。比如如上24次幂的多项式等价于24✖24的状态转移矩阵A✖[Q1…Q24]的寄存器一维序列,就是下一次寄存器序列的数值。  Phase Shifter:电路介绍 Phase Shifter: 通常相移器用于减少从发生器输出的序列之间的结构依赖性。当一个Ring LFSR需要驱动许多节点时,为了弥补LFSR本身的随机性不足的劣势,它通常会连接到一个相位移位器上。如下图所示,在没有相移器的情况下,相邻位之间数据流存在对角线关系:但是在加入相移器之后,对角线关系就消失了! 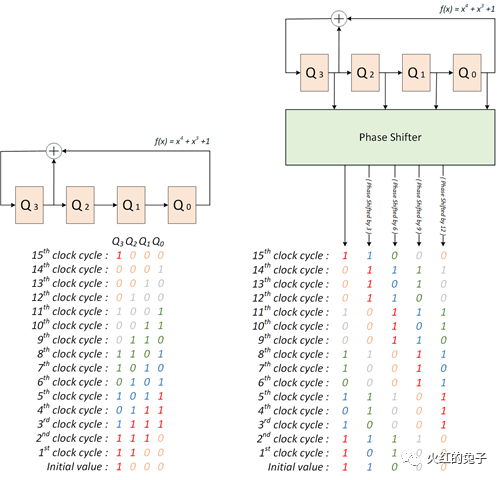 那么为了引入更多的随机性,使用XOR组成的移相器,这样更多的随机性有助于增加故障覆盖率。另外有个附带的重要特点是可以增加更多的节点输出,增加了我们的通道数目! 真实的EDT使用的LFSR的核心解释如上,当然会加入一些优化,比如防止绕线困难等。这里有兴趣的可以直接看EDT的代码。 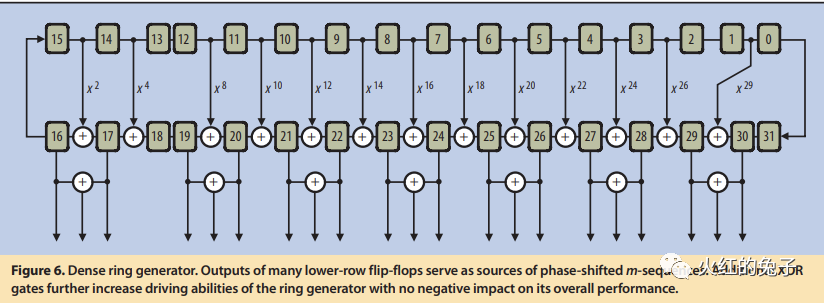 |





