自动测试设备 (ATE)对PLL(锁相环)进行测试时,我们首先要明白PLL在系统级芯片(SoC)中的重要性。它是SoC中关键的时钟或信号同步部件,其性能直接影响到芯片逻辑的正确运行。在测试PLL IP时,通常会有多个测试项目,如频率测试、相位噪声、锁定时间、稳定性、误差和漂移等。但在SoC的ATE测试中,CP阶段通常只进行PLL频率和锁定测试。那么DFT如何产生PLL 测试pattern,以及ATE如何根据这些pattern进行PLL测试? PART01 : DFT 产生 PLL 向量 DFTer 每条PLL向量配置要求:(参考下图) a) JTAG配置多个PLL为对应的待测频点. b) 配置Div系数为最大,尽可能降低输出时钟的频率。 c) LOCK信号在TDO串行移出观测或者复用到IO上。 d) 切换IO复用后,PLL div 信号将会输出到对应GPIO上。 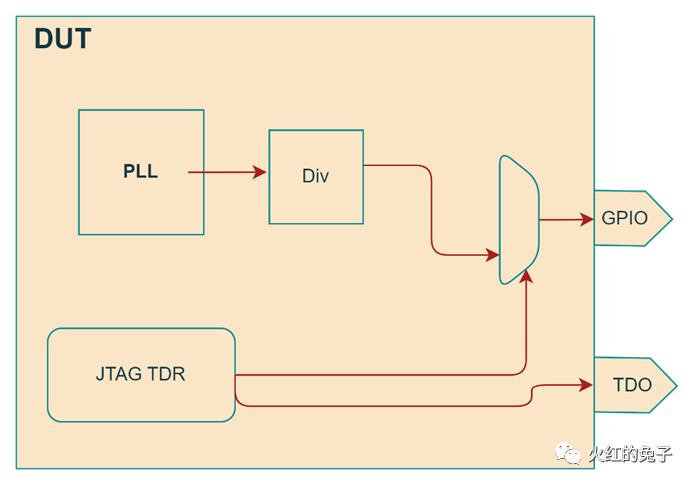 PLL输出频率的要求:10M~50M之间。 WHY? 1. 上限受限于GPIO,在高于50M时,GPIO的输出特性随频率升高而减弱,最好低于50M。(机台PS1600最高1.6G采样频率,不需要考虑奈奎斯特频率的限制。) 2. 下限需要考虑到不同测试方法的测试时间的影响,比如给一个32K的钟,机台需要构造更长的采样向量。 PART02 : ATE如何测试PLL 两种方法: 时域和频域测试,如下: 方法1. ATE time measurement unit ( TMU)测试。(时域,需要额外的TMU license,因此常不采用。) 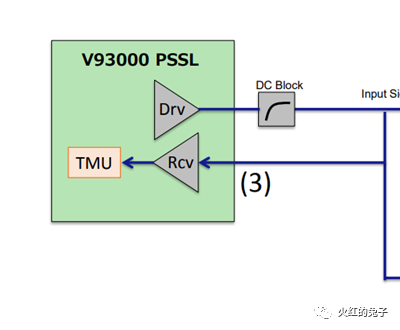 实施步骤:ATE 构造TMU TASK。TMU可以非常高精度地根据task设置trigger到上升沿的时刻,因此可以通过两个上升沿的差值计算出频率,支持多次采样,如下图所示: 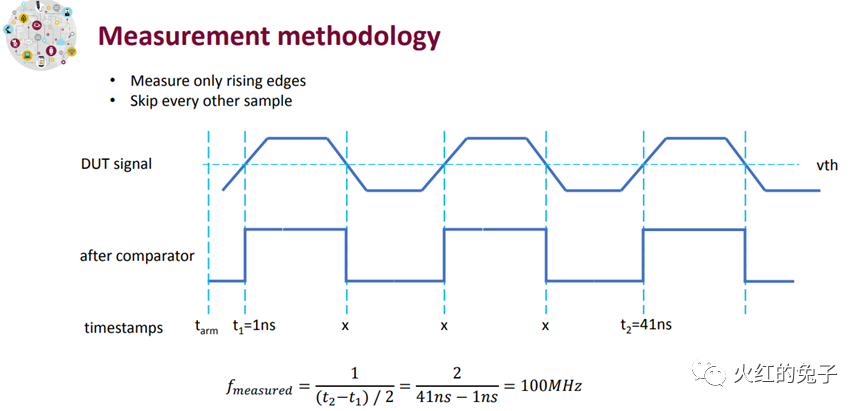 方法2. 构造采样向量,离散傅里叶公式计算频谱,频谱的最大和第2大频率转换即为待测信号频率。(频域) a). 预先构造一条全L的向量,假设叫做PLL_sample. b). 运行DFT PLL向量的测试项.运行后, 不复位的情况下DUT此时稳定输出时钟信号。 c). 运行预先构造好的向量PLL_sample,收集fail cycle,也就是ATE的error map。获得一串0/1组成的一维序列,如下图(点击可放大): 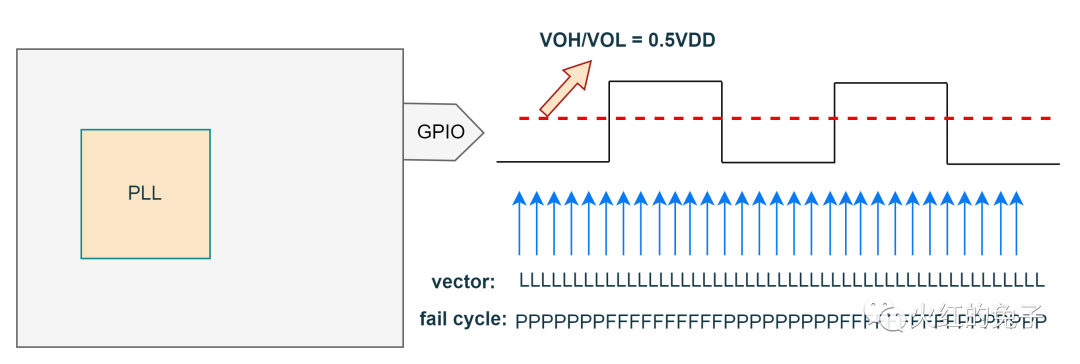 d). 对获得一维序列进行汉明窗口卷积后,使用快速离散傅立叶变换获得频谱。通过频谱可以相当高精度的获得输出的频率,通过spec进行分bin。 如果想了解详情,可以参考论文,这里不再赘述: A Method of High Precision Frequency Detection with FFT, IEIEC Transaction A Vol. J70-A No.5 pp.798-805, May 1987 实际步骤:首先应用DSP_FFT与汉明窗口。然后搜索频谱第一大主频kmax 和第二大频,(kmax-1 或者 kmax+1)。如图所示,第1大和第2大频率成为关键参数。 核心为两个公式: 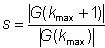 , , 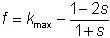  1: int i,kmax,Ndgt,Nsp; 2: double dR,dX,dY,dMax,dFresln,dFx,dFdgt; 3: double dFrequency,dAmplitude,dPhase; 4: COMPLEX CX,CY,CZ; 5: ARRAY_D dVdgt,dSp,dTemp; 6: ARRAY_COMPLEX CSp; 7: 8: dVdgt=DGT("Aout").getWaveform(); 9: Fdgt=1.0/DGT("Aout").getConvClock(); 10: Ndgt=dVdgt.size(); 11: dFresln=dFdgt/Ndgt; // Frequency resolution(bin space) 12: 13: DSP_FFT(dVdgt,CSp,HANNING); // Apply HANNING window 14: Nsp=CSp.size(); 15: DSP_RECT_POL(CSp,dSp,dTemp); // Spectrum length 16: 17: dMax=0.0; kmax=0; 18: for (i=1;i<Nsp;i++) { // Search the maximum length 19: if (dSp[i]>dMax) { dMax=dSp[i]; kmax=i; } 20: } 21: 22: if (dSp[kmax-1]>dSp[kmax+1]) { 23: dR=dSp[kmax-1]/dSp[kmax]; // Equation(12) 24: dFx=kmax+(1.0-2.0*dR)/(1.0+dR); // Equation(16) 25: } else { 26: dR=dSp[kmax+1]/dSp[kmax]; // Equation(17) 27: dFx=kmax-(1.0-2.0*dR)/(1.0+dR); // Equation(18) 28: } 29: dFrequency=dFx*dFresln; // Estimated Frequency 30: // dFx: Estimated Bin Location 31: dX=dFx-kmax; 32: dY=M_PI*dX; 33: dAmplitude=-dSp[kmax]*(dY/sin(dY))*(dX-1.0)*(dX+1.0); 34: // Equation(21) 35: CX=CSp[kmax]; 36: CY.real()=cos(dY); 37: CY.imag()=-sin(dY); 38: CZ=CX*CY; 39: dPhase=atan2(CZ.imag(),CZ.real()); // Equ.(22)[rad] "Quality is never an accident; it is always the result of intelligent effort." - John Ruskin |





