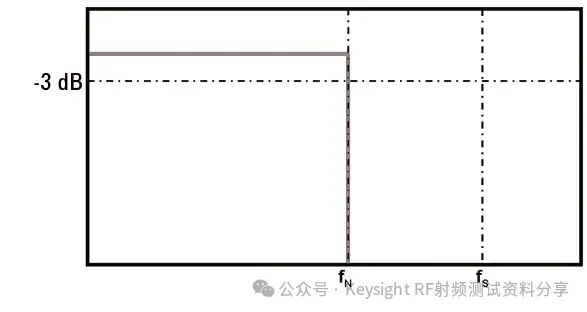
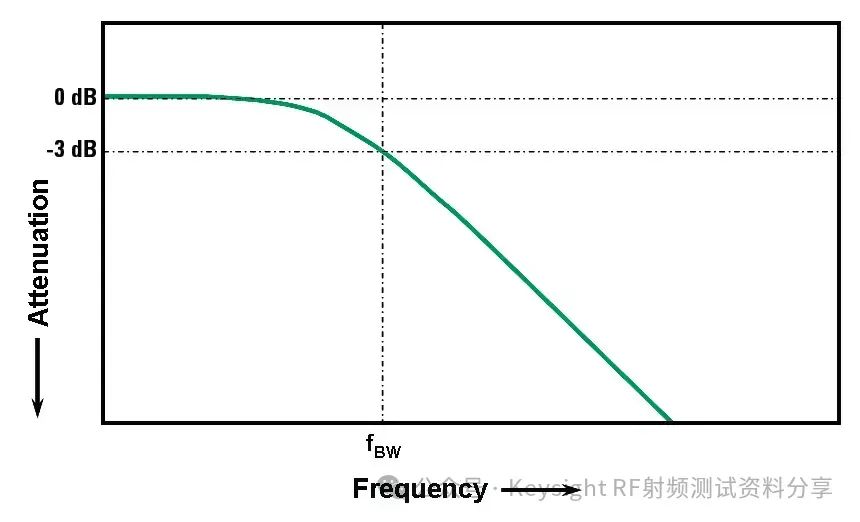
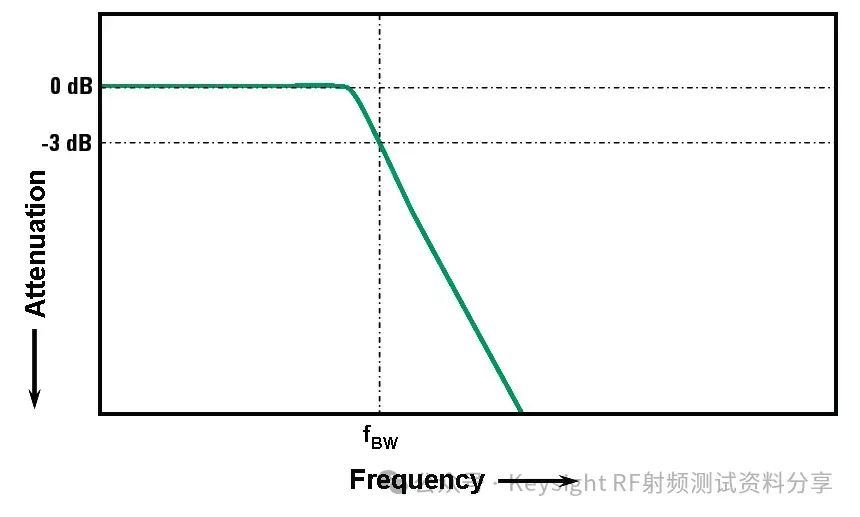
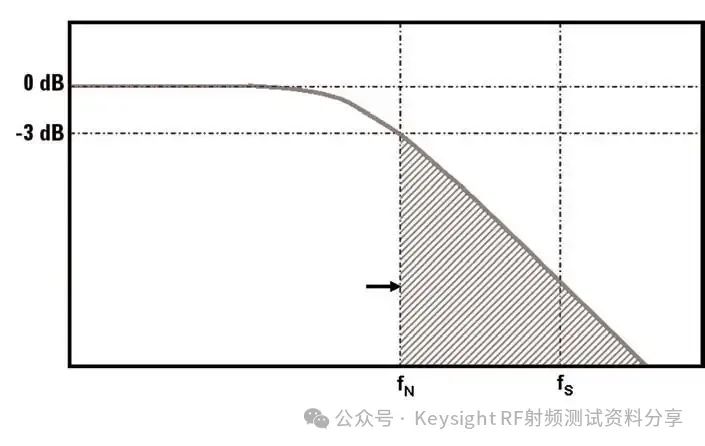
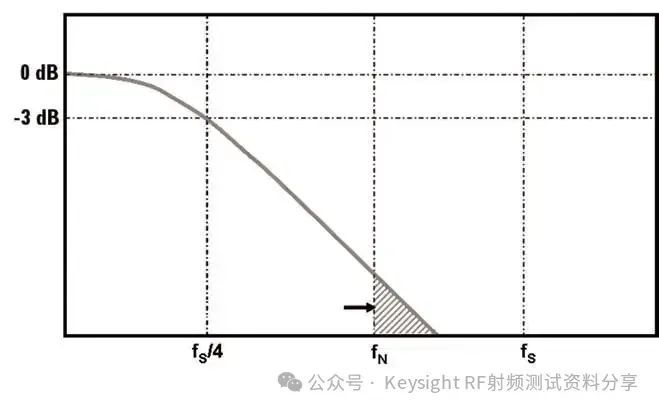
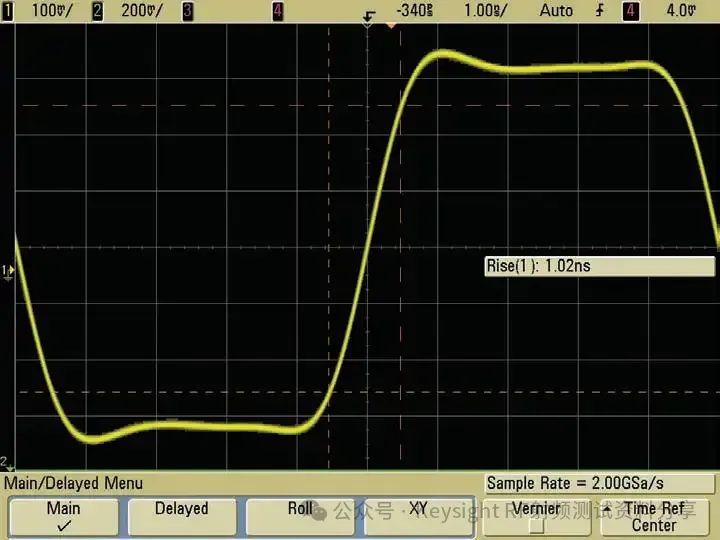
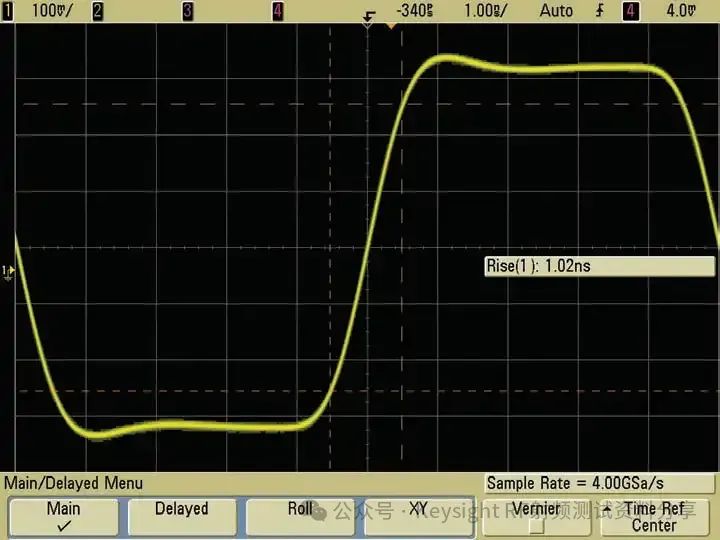
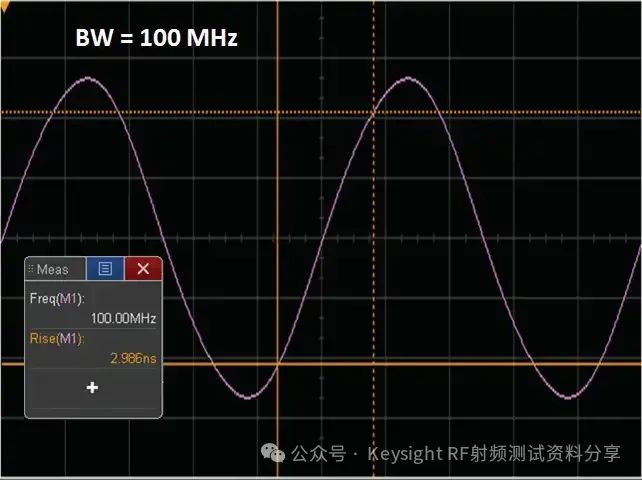
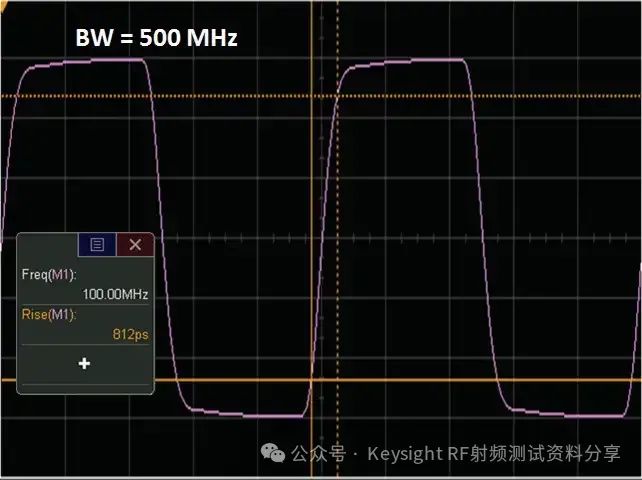
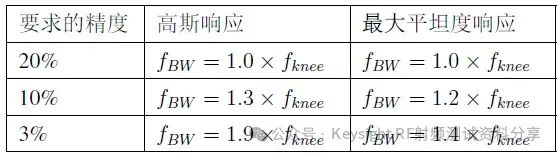
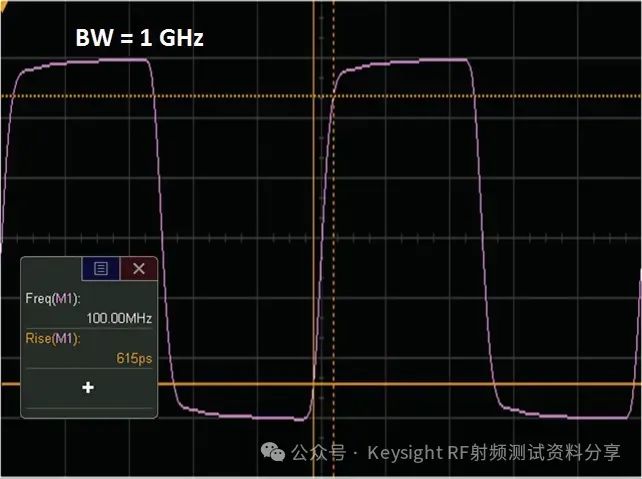
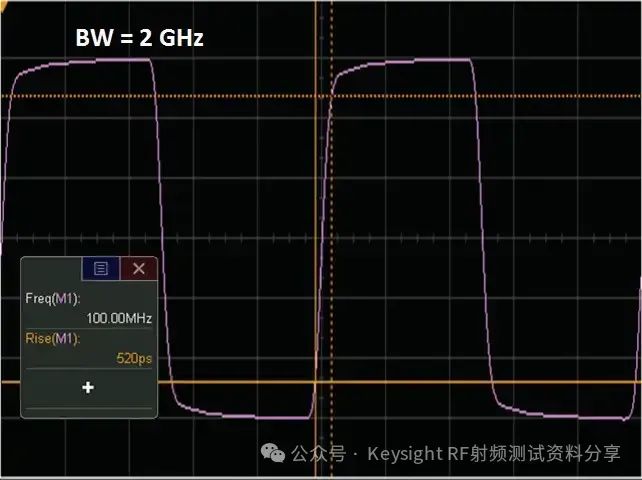
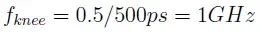带宽和频率的关系到底是什么？示波器带宽怎么_专业集成电路测试网-芯片测试技术-ic test

频率响应作为一个主要参数，我们以示波器为例讨论一下示波器带宽与频率响应的关系。

是德科技示波器 (原安捷伦示波器) 校准主要参数包括：

——水平扫描时间：显示准确度，考察晶体振荡器的性能
——上升时间Tr（瞬态响应）：越短越好，可快速捕捉瞬时信号
——频率响应（稳态响应）：更进一步考察给的宽带余量
——输入阻抗

示波器有很多不同性能指标规格，确定了可捕获和测量信号的准确度。在介绍示波器性能指标之前我们先看一下Nyquist 采样定理。

Nyquist 采样定理

现实世界接触到的诸如电信号、光信号、声音信号等这些信号都是随时间连续变化的，称之为连续信号。但对于计算机来说，处理这些连续的信号显然是无能为力，要使计算机能够识别、计算、处理这些连续信号就必须将其转化为离散信号，将连续信号转换为离散信号的过程就叫采样。采样后，计算机得到的是离散的点，用这些离散的点来代替连续的线就势必会产生误差，那么怎么采样才能使得这个误差在可以接受的范围内呢？这就引出了Nyquist 采样定理。

我们首先从简单的开始，对于一个正（余）弦信号的曲线，我们并不需要将曲线上面每一点都记录下来，只需要就一些特殊点就够了，比如相邻两个零点的位置（图上红色的两个点）或者相邻的波峰和波谷的位置（图上绿色的两个点），只要是按照正（余）弦信号的规则，就能够根据这些特殊点还原出正（余）弦信号，用香农信息论的观点来看就是这两个点已经包含了正（余）弦信号的信息熵，两个点足矣。也就是说，正弦信号周期为1，两个采样点，无论是相邻的两个零点还是相邻的波峰与波谷位置的间隔都是0.5，因此，可知采样的周期为0.5，恰好为正弦信号周期的一半。也就是说采样频率为该正（余）弦信号频率的2倍，我们就可以恢复出这个正（余）弦信号。请大家先记住这个结论。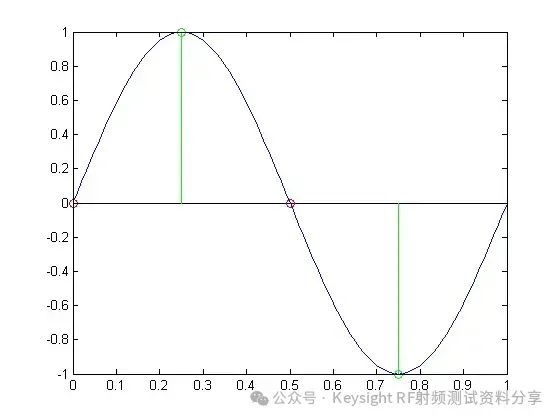

Nyquist 采样

示波器采样率

根据 Nyquist 采样定理，只要采样频率大于信号最大频率的2倍，我们就可以通过采样点信息将信号恢复出来。那么示波器最重要的指标是不是就是采样率了？我们测量信号只需要看采样率就行了？

这里我们举一个例子，下图显示用一个500-MHz 带宽的示波器以 1 GSa/s的速度对100MHz的时钟信号进行采样。这个输入信号的基本频率（时钟频率）远低于500MHz，。但是如果仔细查看会发现，该信号的边沿具有不同程度的预冲、过冲和各种边沿速度，呈现出“不稳定”的趋势。这是为什么呢？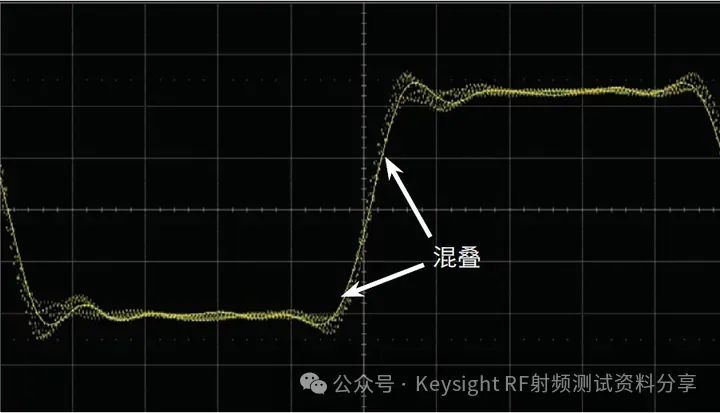

使用 1 GSa/s 采样率和 500-MHz 带宽的示波器进行采样所产生的混叠边沿

在分析这个问题之前，我先给大家普及一个基本常识。我们知道任何的信号最终都可以表示为正（余）弦信号的线性组合。比如我们比较熟悉的方波是由多个正弦信号叠加而成。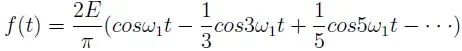

我们仅取一次波，三次谐波和五次谐波，可以得到如下图所示波形。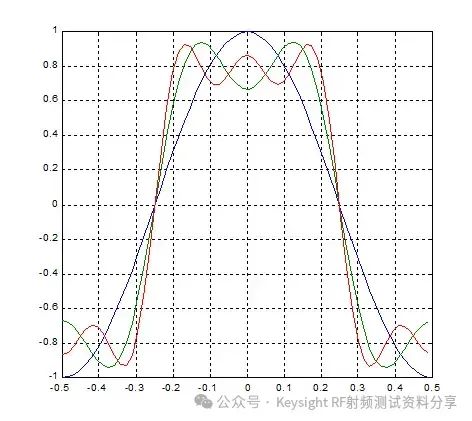

由一次波，三次谐波和五次谐波组成的方波

如果我们取到11此谐波，如下图所示，那么波形就更加趋近理想方波。当我们区无限次谐波，就可以得到一个理想方波。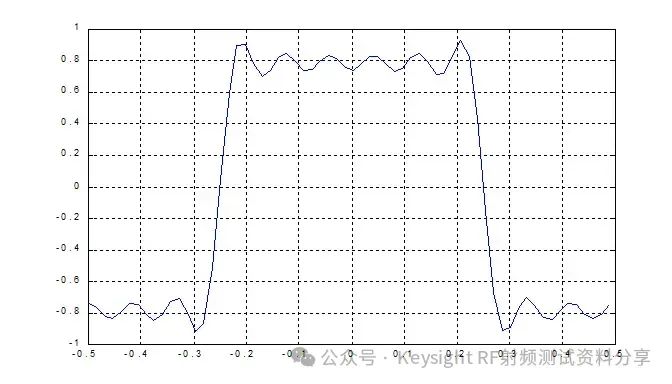

由一次波到十一次谐波组成的方波

也就是说一个方波包含无限高频率的频率成份，只是越高的频率成分所包含的频率分量的能量越小。

我们回到之前的这个问题，对于一个100MHz的时钟方波，它包含有100MHz的基波，300MHz的三次谐波，500MHz的五次谐波，700MHz次谐波等等的各次谐波。那么1GSa/s的采样率最多可以正确采样500MHz的五次谐波，无法正确采用700MHz及以上频率的谐波，那么也就使得测量结果出现一些不定态，这就是混叠的迹象。

也就是说如果只是关注采样率，我们采很多信号都会出现问题，那是因为我们还需要关注一个更重要的指标：示波器带宽。

示波器带宽什么意思?

其实信号进入示波器以后都要进过一个滤波器，这个滤波器的带宽就是示波器的带宽。当信号输入频率接近示波器的指定带宽时，测得的幅度会慢慢下降。信号在带宽频率下将会衰减 3 dB（~30\%）。也就是说信号通过一个滤波器先将一些高频信号过滤出去，然后再进行采样，这样就不会出现混叠现象了。

那是不是说只要采样频率是示波器带宽的2倍就可以了呢？如果示波器带宽恰好指定为 Nyquist（fN），则意味着示波器具有理想的砖墙式（brickwall）响应，该响应在此相同频率下会完全衰减（如图\ref{ref_brickwall} 所示）。低于Nyquist 频率的频率分量会完全通过（增益 =1），高于 Nyquist 频率的频率分量则会完全予以排除。然而，这种频率响应滤波器无法在硬件中实施。

理想的砖墙式频率响应

实下降特征、更为平坦的带内响应，如图

示波器高斯频率响应

带宽技术指标大于 1 GHz 的示波器通常拥有最大平坦频率响应。这类响应通常在 -3 dB 频率附近显示出具有更尖锐下降特征、更为平坦的带内响应，如下图：

示波器最大平坦度频率响应

如果示波器的带宽正好指定为 Nyquist（fN）（如下图所示），输入信号超过这个频率的分量尽管衰减超过 3 dB，但也被采样（红色阴影部分），尤其当输入信号中包含快速边沿时，情况更是如此（测量数字信号时）。这种现象违背了 Nyquist 采样定理的第一条规则。

带宽（fBW）指定为 Nyquist 频率（fN）时，典型的示波器高斯频率响应

大多数示波器厂商不会将示波器的带宽指定在 Nyquist 频率（fN）。之前的例子已清晰表明仅仅使用带宽为采样率 2 倍的示波器还不足以获得可靠的数字信号测量结果。

那么，示波器的带宽（fBW）的定义应该怎么关联到波器的采样率（fS）和Nyquist 频率（fN）呢？为了尽量避免对超出 Nyquist 频率（fN）的频率分量进行采集，大多数示波器厂商将其具有典型高斯频率响应的示波器带宽指定为实时采样率的 1/4 至 1/5 或更低（如下图所示）。

将示波器带宽（fBW）限制为采样率的 1/4（fS/4），可以降低 Nyquist 频率（fN）之上的频率分量

尽管以比示波器带宽大更多倍的速率采样可以进一步降低采集 Nyquist 频率（fN）之外频率分量的可能性，但是 4:1 的采样率与带宽比足以获得可靠的数字测量结果。带宽技术指标在 2-GHz 和更高范围的示波器通常具有更陡峭的频率衰减响应特征。我们将这种类型的频率响应称为“最大平坦度”响应。由于具有最大平坦度响应的示波器接近于砖墙式滤波器的理想特征，在这种情况下，超出 Nyquist 的频率分量衰减程度更高，因此无需进行多次采样即可很好地显示使用数字滤波的输入信号。理论上厂商可以将具有此类响应的示波器带宽（假设前端模拟硬件具备相应能力）指定为 fS/2.5。

下图显示了500-MHz 带宽的示波器捕获边沿速度在 1 ns（10% - 90%）范围的100-MHz 的时钟信号。500 MHz的带宽技术指标是精确捕获此数字信号的最小推荐带宽。这一特定的示波器能够在双通道工作模式下以 4 GS/s 进行采样，或者在三或四通道工作模式下以 2 GS/s 进行采样。下图显示频率（fN）的两倍，带宽频率（fBW）的四倍。该图表明，采样率与带宽之比为 4:1 的示波器可以非常稳定而准确地表示输入信号。并且，借助Sin(x)/x 波形重建/ 插值数字滤波技术，此示波器的波形和测量分辨率可达几十皮秒的量级。与我们之前图\ref{ref_sampel_large_bandwidth}所显示的例子（采用相同带宽的示波器，但仅为带宽（fN）两倍的速度进行采样）相比，波形稳定性和精确度的差别显而易见。

采用是德科技 500-MHz 带宽示波器以 2 GSa/s 的速率进行采样，可以精确测量这个边沿速度为 1ns 的 100-MHz 时钟信号

那么，如果我们将采样率增大一倍，使其达到 4 GSa/s，再以相同的 500-MHz 带宽示波器（fBW x 8）采样，结果又会怎样呢？您可能会直观地认为该示波器将会获得更佳的波形和测量结果。但正如图所示，您只能取得很小的改进。如果仔细观察这两个波形图，您将会发现，以 4 GSa/s（fBW x 8）采样时，显示的波形中仅有轻微的预冲和过冲。但是，上升时间测量显示相同的结果（1.02ns）。

采用是德科技 500-MHz 带宽示波器以 4 GSa/s 采样，与 2 GSa/s 采样相比，对测量效果的提高微乎其微

需要了解更多带宽和频率的关系，请扫描二维码, 阅读应用文章：频率响应是什么？

示波器带宽怎么选择？

前面介绍了带宽与采样率的关系，知道示波器关键的指标还是带宽。那和确定示波器带宽的选择呢？

前面提到所有示波器都会在较高频率时出现低通频率响应衰减。大多数带宽技术指标在 1 GHz 及以下的示波器通常会出现高斯响应，并在 -3 dB 频率的三分之一处表现出缓慢下降特征。带宽技术指标大于 1 GHz 的示波器通常拥有最大平坦频率响应。这类响应通常在 -3 dB 频率附近显示出具有更尖锐下降特征、更为平坦的带内响应。无论示波器具有高斯响应、最大平坦度响应或介于二者之间的响应，输入信号衰减 3 dB 所在的最低频率称为示波器的带宽。使用正弦波信号发生器，在扫描频率上测试示波器的带宽和频率响应。信号 -3 dB 频率处衰减约为 -30% 幅度误差。所以当信号的主要频率接近示波器的带宽时，很难对信号进行非常精确的测量。

根据以往经验，示波器带宽应比被测系统的最快数字时钟速率至少快5倍。如果示波器满足这一标准，则其能够捕捉高达5次的谐波，并实现最小的信号衰减。
下图显示了使用 100 MHz 带宽示波器对边沿速度（10% 至 90%）为 500 ps 的 100 MHz 数字时钟信号进行测量获得的波形结果。如图所示，示波器仅允许该时钟信号的 100 MHz 基本波形通过，从而将时钟信号显示为近似正弦波。显然测量 100 MHz 时钟信号，100 MHz 带宽示波器就无能为力了。

使用100MHz带宽示波器捕获100MHz时钟信号

500MHz带宽示波器能够捕获5次谐波，因而成为我们首选500MHz或以上带宽的示波器。500MHz带宽示波器测量结果如下图所示：

使用500MHz带宽示波器捕获100MHz时钟信号

我们看到测试结果已经是一个不错的方波了，但是当测量上升时间时，我们看到示波器测得的结果为大约800ps。在这种情况下，示波器无法非常精确地测量此信号的上升时间。示波器实际上测量的是接近于自身上升时间（700 ps）的目标，而不是输入信号的上升时间（500 ps 左右）。这显然和我们要测的信号之间有较大的误差，这是为什么呢？

一般信号的边沿包含更多的高频信号。当包含的高频信号越多，上升沿越快。这里我们的被测信号有比较陡峭的上升沿，也就是说信号有比较多的高次谐波分量，但是由于示波器的带宽限制，5此以上谐波分量都受到了比较大的衰减，使得示波器显示的信号边沿陡峭度下降。那么如果想精确测量被测信号，我们就需要确定被测数字信号中出现的最高频率，而不是最大时钟速率。最高频率将由设计中的最快边沿速度决定。所以要做的第一件事就是确定最快信号的上升时间和下降时间。

您可以使用一个简单的公式来计算最大的“实际”频率分量。Howard W. Johnson 博士已经针对此主题撰写了一本书《Highspeed Digital Design – A Handbook of Black Magic》。他将这个频率分量称为 " 拐点" 频率 (fknee)。所有快速边沿都有无穷多的频率分量。然而，在快速边沿的频谱图中有一个曲折点（或“拐点”），此处高于 fknee 的频率分量对于确定信号的波形影响不大了。拐点频率的计算公式如下：

知道拐点频率以后，我们可以根据自己的期望测量准确度来确定示波器的带宽要求，具体的乘积系数如下

我们现在回头来看一下前面的例子：信号具有近似 500 ps 的上升/ 下降时间（基于 10% 至 90%标准），那么信号中的最大实际频率分量（fknee）将大约等于 1GHz。

如果在对信号进行实际的上升时间和下降时间测量时，您能够容忍最多 20% 的计时误差，那么可以使用 1 GHz 带宽示波器用于数字测量应用。

带宽 = 1.0 X 1 GHz = 1.0 G

但是如果需要 3% 左右的计时精度，则最好使用2 GHz 带宽的示波器。

示波器带宽 = 1.9 X 1 GHz = 1.9 G

借助 1 GHz 带宽示波器，我们可以获得更精确的信号图形（如下图所示）。当测量上升时间时，我们看到示波器测得的结果大约为 600 ps。这个测量为我们提供大约 20% 的测量精度。如果想要以超过 3% 的精度和500ps的边沿速度对信号进行测量，我们确实需要使用2 GHz 及以上带宽的示波器（通过之前的示例确定了这一数值）。如下图所示，2GHz 带宽的示波器能够更精确地显示这个时钟信号，同时非常准确地测量上升时间（约 520 ps）。

使用 1 GHz 带宽示波器捕获 100 MHz 时钟信号

使用 2 GHz 带宽示波器捕获 100 MHz 时钟信号

示波器带宽与示波器频率响应的关系

频率响应是什么意思？

系统对正弦输入信号的稳态输出响应称为频率响应。线性时不变系统在正弦输入信号的激励下到达稳态后，其输出信号仍为正弦信号，且频率与输入信号相同，但幅值和相位可能发生变化。系统对不同频率的正弦输入产生的不同输出响应中，我们主要关注幅值和相位随信号频率的变化。

对于输入信号：

搜索

热门标签: