1、零点和极点的定义假设我们有一个传递函数,其中变量s出现在分子和分母中。在这种情况下,至少一个s值将使分子为零,并且至少一个s值将使分母为零。使分子为零的值是传递函数零点,并且使分母为零的值是传递函数极点。让我们考虑以下示例: 在这个系统中,在s=0时为零点,在s=–ω0时为极点。极点和零点定义了滤波器的特征。如果你知道极点和零点的位置,则可以获得有关系统如何响应不同输入频率的信号的信息。 2、极点和零点的影响 波特图提供了极点或零点与系统输入与输出行为之间关系的直观可视化。 在电路理论和控制系统工程中,零点(zeros)和极点(poles)是描述系统动态特性的重要概念。它们对系统的波特图(Bode plot)有着重要的影响。 (1)极点对波特图的影响: 极点是系统传递函数中使得分母为零的值。它们在波特图上表现为增益的下降(negative slope)。极点越靠近低频,对应的增益越高,而在高频时增益较低。在极点附近,相位角变化也较大,可以引起系统的相位延迟。 如果我们把两个电阻串联在一起,如图10.17所示,通过电阻分压获取一个输入输出的关系,是一个跟频率无关的比例输出。  图 10.17 电阻分压电路 这个电路的传递函数跟频率无关,H(s)跟s无关。  因为电阻不会随着频率变化而变化,所以H(s)始终是个常数,体现在波特图上面,增益和相位都是一条直线,如图10.18所示。  图 10.18 电阻分压电路的波特图 我们知道电容的阻抗是跟频率相关的,我们把电阻分压电路中的R2更换为一个电容变成一个RC电路,如图10.19所示。 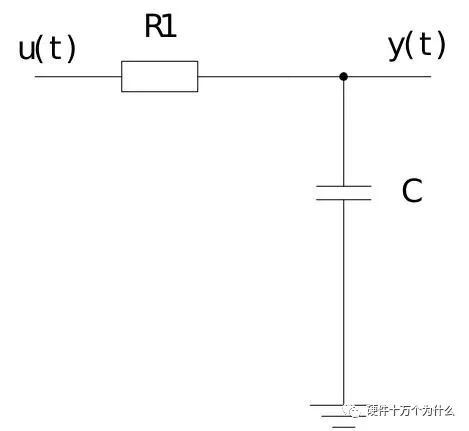 图 10.19 RC电路 其传递函数,是电阻和电容的阻抗进行分压:  极点是传递函数的分母中使得传递函数为零的点。为了找到极点,我们让分母等于零:1+sCR1=0 这表明极点是  截止频率表示信号的频率分量被滤波器弱化的点。对于一阶RC低通滤波器,截止频率的绝对值是  。 。我们忽略了虚部的负号,因为在实际应用中,我们通常只关注频率的绝对值。 我们计算RC电流的幅频特性和相频特性: 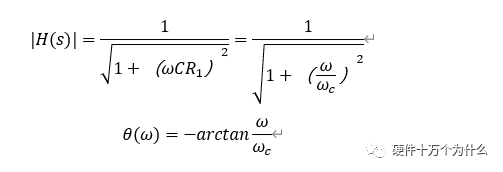 RC低通滤波器的幅频特性图和相频特性图,如图10.20所示。 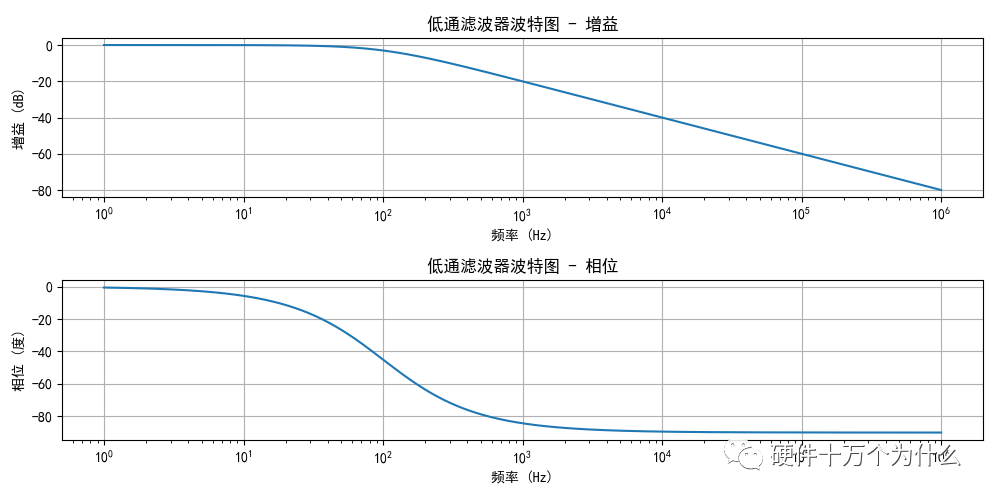 图 10.20 一阶RC低通滤波器波特图 (2)零点对波特图的影响: 零点是系统传递函数中使得分子为零的值。它们在波特图上表现为增益的上升(positive slope)。零点越靠近高频,对应的增益越高,而在低频时增益较低。在零点附近,相位角变化较大,可以引起系统的相位提升。 我们把分压电路中的R1更换为C怎形成一个一阶高通滤波器,如图10.21所示。  图 10.21 一阶RC高通滤波器波特图 其传递函数,是电容和电阻的阻抗进行分压:  对于这个传递函数,零点是使得分子等于零的复数s 的值。分子有一个可以为0的s值就是s=0,所以零点为s=0。 极点是使得分母等于零的复数s 的值。分母有一个可以为0的s值,。因此,一阶RC高通滤波器的零点是原点 s=0,而极点是  。 。RC低通滤波器的幅频特性图和相频特性图,如图10.22所示。  图 10.22 一阶RC低通滤波器波特图 (3)零极点影响波特图的斜率 我们常常使用复数形式的频率表示。复数具有实部和虚部,而在实际应用中,我们更关注频率的绝对值。在电路分析中,当我们考虑阻尼比、共振频率等信息时,我们会使用复数频率。 我们在实际工程中,往往会忽略具体的传递函数和幅频特性曲线和相频特性曲线。只需要把每一个零点和极点找到,标记出来,然后按照这个原则修改波特图的斜率就可以完成波特图的渐近线:极点频率对应的频率,在频率处,振幅曲线的斜率减小20dB /dec,并且一个零点对应于一个角斜率,在该频率下,斜率增加20dB /dec,如图10.23所示。  图 10.23 波特图及其渐近线的关系图 对于一阶RC低通滤波器的极点,它是一个复数,具有零实部和负虚部。在频域分析中,这个负的虚部表达了一个衰减的振荡,但在实际应用中,我们通常关注的是频率的绝对值。所以我们说的零点是传递函数为0,传递函数为0时传递函数的绝对值不是零,表现出来不是传递函数为0,而是传递函数的斜率发生了变化。 极点频率对应于角频率,在该角频率处,振幅曲线的斜率减小20dB /dec,并且一个零点对应于一个角斜率,在该频率下,斜率增加20dB /dec。"dec" 是 "decade" 的缩写,表示一个数量级的变化。在对数尺度中,一个 decade 意味着频率或幅度变化了一个数量级,即增加或减小了10倍。因此,+20dB/dec 表示每增加一个 decade 的频率,增益增加 20dB。这种标记方式通常在描述频率响应的变化时使用,特别是在滤波器和系统分析中。 在音频工程和信号处理中,通常使用对数尺度来表示频率。对数尺度的一个关键特性是,每个数量级(10的幂)的变化都对应一个固定的增益。对数尺度上,以dB(分贝)为单位的增益变化与频率的对数关系是线性的。 对数尺度中,1 Hz到10 Hz的变化是一个数量级,10 Hz到100 Hz也是一个数量级,以此类推。对数尺度中的一个数量级变化对应于一个10倍的频率变化。由于对数的性质,这样的变化可以用一个线性的斜率来表示。 当你在增益曲线上观察到+20dB/dec的斜率时,这意味着每增加一个数量级的频率,增益就会增加20dB。这是因为对数尺度中的每个数量级变化对应于10倍的频率变化,而20dB正好是10的对数的两倍。 因此,+20dB/dec的斜率代表了在对数尺度上频率的线性变化。这种特性在许多电子滤波器和系统的频率响应中很常见,特别是在Bode图中。 (4)零极点影响波特图的斜率为什么正好是±20dB/dec? 零极点对于波特图(Bode Plot)斜率的影响涉及到频率响应的数学性质。波特图是一种常用于表示线性时不变系统频率响应的图表,通常以对数刻度绘制。 在一阶系统中,当存在一个零点或极点时,频率响应在那一点会发生-20dB/dec的斜率变化。这是因为对数刻度下的斜率变化是以10为底的对数刻度,而一阶系统的频率响应可以用以下的一般形式表示:  其中N(jω) 和D(jω) 分别是分子和分母的多项式, j 是虚数单位,ω 是频率。在jω 平面上,零点是使得分子为零的点,极点是使得分母为零的点。在对数刻度下,频率响应 20log10∣H(jω)∣可以表示为:  在零点处,N(jω) 为零,则只剩第二项,斜率为 -20dB/dec。同样,在极点处,D(jω) 为零,只剩第一项,斜率为20dB/dec。所以有: 极点(Pole):在极点处,频率响应的振幅曲线的斜率减小。对于一阶系统,当角频率达到极点时,振幅曲线的斜率减小 20 dB/dec。这表示系统对该频率的信号的衰减更慢。 零点(Zero):在零点处,频率响应的振幅曲线的斜率增加。对于一阶系统,当角频率达到零点时,振幅曲线的斜率增加 20 dB/dec。这表示系统对该频率的信号的衰减更快。 零极点体现在波特图中斜率的变化,如图10.24所示。  图 10.24 波特图渐近线变化斜率 正因为曲线变化的频率点确定,并且变化的斜率也确定,则我们只需要找出零极点所在位置,更改斜率,就可以绘出波特图的渐近线,用于分析环路的关键特性了。 (5)零点和极点共同影响 零点和极点的数量和位置共同决定了系统的频率响应特性。它们对系统的稳定性、响应时间和频率选择性等方面都有影响。在频率响应图上,零点和极点的位置决定了幅频特性(增益)和相频特性(相位)。如果是双重极点,或者双重零点则斜率变化翻倍。 (6)相位裕度和增益裕度 相位裕度和增益裕度是系统稳定性的指标,它们与零点和极点的分布有关。如果系统的相位裕度和增益裕度足够大,系统就更加稳定。零点和极点的位置对相位裕度和增益裕度有直接影响。总体来说,零点和极点的位置和数量对系统的频率响应有着重要的影响,直接影响系统的稳定性、性能和动态特性。最终我们在调试电源的环路稳定性的时候就是通过增加零点和极点的数量和位置来实现我们期望的相位裕量和增益裕量。 3、隐藏的零点 低通滤波器的传递函数可以写成如下: 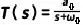 这个系统有零点吗?如果我们应用本文前面给出的定义,将得出结论,它不是变量s不出现在分子中,因此s的任何值都不会导致分子等于零。事实证明,它确实有一个零点,为了理解原因,我们需要考虑传递函数极点和零点更一般化的定义:零点(z)发生在s的值上,它导致传递函数减小到零,极点(p)发生在s的值上,导致传递函数趋向于无穷大。 一阶低通滤波器的s值会导致T(s)趋于0,这个值就是s =∞。因此,一阶低通系统在ω0处有极点,在ω=∞处有零点。我们尝试在ω=∞处提供零点的物理解释:它表示滤波器不能继续“永久”衰减(其中“永久”指的是频率,而不是时间)。如果设法创建一个输入信号,其频率继续增加直到达到无穷大rad / s,则s =∞时的零点会使滤波器停止衰减,即振幅响应的斜率从-20 dB /dec变为0 dB /dec。 4、相移的特性 在探讨零点和极点对系统相移的影响时,我们需要了解它们在复平面上的位置。相位是极坐标表示中的角度,而零点和极点在复平面上是复数,可以通过极坐标 rejθ 来表示,其中 r 是模长,θ 是相位角。 对于零点和极点,它们的相位角分别是90度和-90度(或270度)。这是因为它们通常位于虚轴上,即复数的实部为零。虚轴上的点的相位角是90度或-90度,具体取决于它们在上半平面还是下半平面。 零点:零点通常位于虚轴上,相位角为90度。这是因为零点对应于分子的根,而在分子中,当 s 等于零时,分子的实部为零,因此它们通常位于虚轴上。 极点:极点通常也位于虚轴上,相位角为-90度。这是因为极点对应于分母的根,而在分母中,当 s 等于零时,分母的实部为零。 这些相位角的差异导致了在零点和极点附近频率响应的相位变化。在频率响应曲线中,当通过零点时,相位增加90度;当通过极点时,相位减少90度。这是频率响应曲线上出现相位移的原因。 由极点产生的相移的波特图近似是表示相移的-90°的直线。该线以极点频率为中心,并且每十倍频率下具有-45°的斜率,这意味着向下倾斜的线在极点频率之前十倍频率开始并且在极点频率之后十倍频率结束,如图10.25所示。除了线具有正斜率之外,零点影响是相同的,使得总相移是+ 90°。  图 10.25 相移特性示意图 |





