 Lbist的组成部分 片上lbist一般由三部分组成：BIST controller、TPG (Test Pattern Generator)、RA (Response Analyzer)。 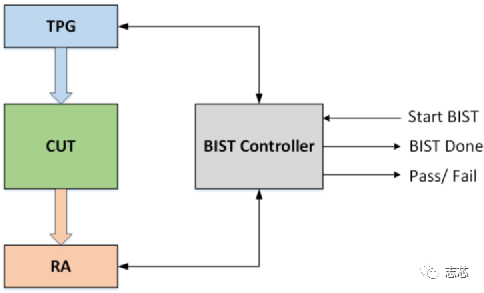 图1 lbist组成示意图 LBIST 的基本机制是它使用线性反馈移位寄存器 (LFSR，Linear Feedback Shift Register) 生成设备内部扫描链的输入，启动一个功能周期，使用多输入签核寄存器（MISR，multiple input signature register ）来捕获设备的响应，并将捕获的响应压缩。来自 MISR 的压缩后的响应称为签核。输出签核中的任何异常都表明设备存在缺陷。 线性反馈移位寄存器 (LFSR) 是一种移位寄存器，其输入位是其先前状态的线性函数。最常用的单位线性函数是异或（XOR）。因此，LFSR 通常是一个移位寄存器，其输入位由整个移位寄存器值的某些位的 XOR 驱动。LFSR 的初始值称为种子，由于寄存器的操作是确定性的，因此寄存器产生的值流完全由其当前（或先前）状态决定。同样，由于寄存器具有有限数量的可能状态，它最终必须进入一个重复周期。但是，具有精心选择的反馈函数的 LFSR 可以产生一系列看起来随机且周期很长的位。LFSR 的应用包括生成伪随机数、伪噪声序列、快速数字计数器和白化序列。 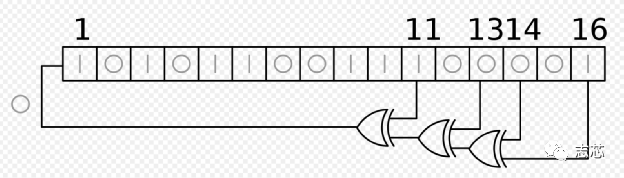 图2 一种16位的LFSR Test Pattern Generator 通常，标准形式的 LFSR 用于生成伪随机pattern，该pattern充当输入测试向量。如图3所示，LFSR中每一个触发器都馈送一条扫描链。在伪随机pattern中，pattern在一定时间间隔后会重复，这就是我们称之为“伪随机”的原因。 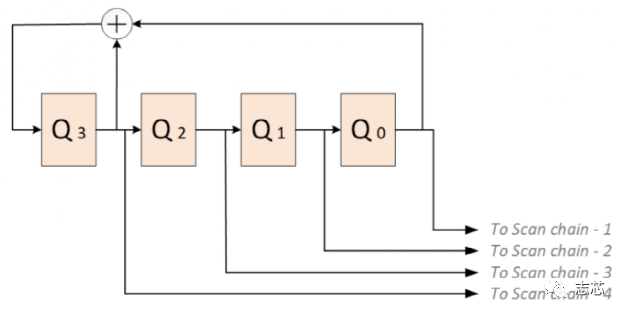 图3 由四个触发器和一个XOR组成的馈送四条链的LFSR LFSR 可以由其特征多项式表征，假设我们使用“1”“0”“0”“0”的输入初始化两个如下图所示的两个4 degree的具有如图所示的多项式的的LFSR。 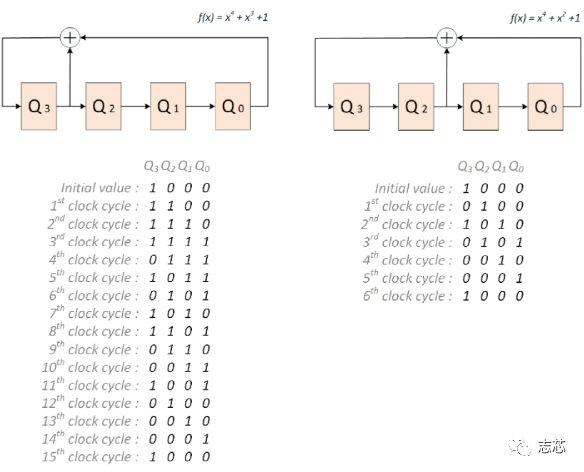 图4 两种不同的LFSR的输出值 具有特征多项式 f(x) = x4 + x3 +1 的 LFSR 生成的pattern在 15 个pattern之后重复，因此具有 24 – 1 = 15 的周期。但是具有特征多项式 f(x) = x4 + x2 +1的 LFSR 生成的pattern在 6 个pattern后重复。 如果 LFSR 有N个触发器（也称为N degree LFSR ），如果其产生的pattern的周期 为2N – 1，则 LFSR 称为maximum-length sequence 或者 m-sequence。将 m-sequence LFSR的特征多项式称为本征多项式。对于给定的 N degree LFSR，本证多项式不是唯一的；例如 – x4 + x3 +1 和 x4 + x3 +1 都是 4 degree LFSR 的本征多项式。 LFSR的多项式的选择对循环长度有很大的影响。更好的周期长度意味着更好的 TPG，因此实现本征多项式的 LFSR 最适合测试pattern生成。 为什么需要移相器 LFSR 的主要缺点之一是没有足够的随机性。考虑我们之前讨论过的相同的 m-sequence LFSR f(x) = x4 + x3 +1。如图5所示，在没有移相器的情况下，相邻比特流（bit stream）之间存在对角关系。 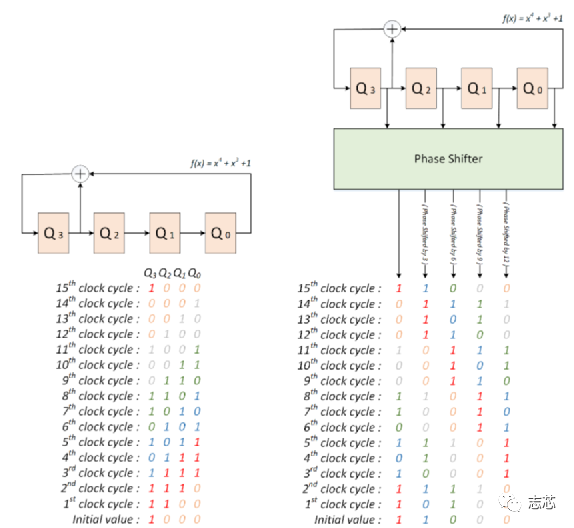 图5 移相器的作用 为了在比特流（bit stream）之间引入更多随机性，我们使用了一个由 XOR 网络实现的移相器。基本上每个比特流（bit stream）都相移了一些周期。正如我们在移相器的存在下所看到的，对角线关系不再存在。更多的随机性有助于增加故障覆盖率。同样正如我们在示例中看到的，4 degree LFSR 正在馈送 5 个扫描链。因此，带有移相器的 LFSR 可以支持更多的扫描链（通常一个“N” degree LFSR 可以支持最多“N”个没有移相器的扫描链）。 如何找到符合要求的LSFR的初始值 我们将使用如下示例示范如何找到LSFR的初始值。 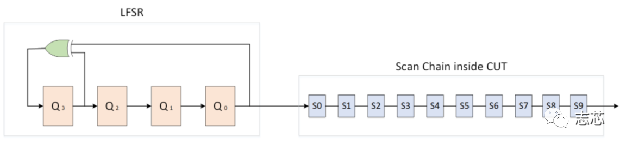 图6 4 degree LSFR馈送10个触发器组成的扫描链 4 degree LSFR馈送10个触发器组成的扫描链，S0-S9 是 ATPG 指定的test pattern，Q0-Q3 是 LFSR 的seed。 有两种方法：1. 逐周期追踪； 2. 线性方程组。 我们将只讨论线性方程组的求解。我们可以在线性方程组中对上述情况进行建模。 注意：S0-S9 值将被串行加载到链中，这样 S9 将在第一个时钟周期首先加载到链中，然后在下一个时钟周期向右移动，同时 S8 将加载到链中.这将持续 10 个时钟周期，直到所有值都加载到所需的位置。 初始条件（S9 是从 LFSR 到链的第一个输入，因此等于 Q0，并且类似地直到 S6）： S9 = Q0 S8 = Q1 S7 = Q2 S6 = Q3。 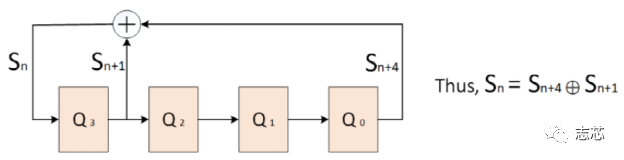 图7 该LFSR中的输入输出关系 看到这个线性方程，想起了高中数学的最后一题，数组方程的归纳推导。 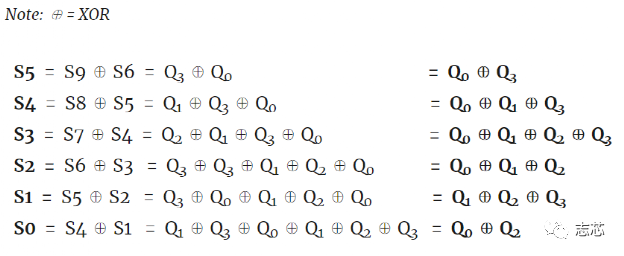 因此一共有 10 个等式方程和 4 个变量 Q0、Q1、Q2 、 Q3。 假设这些pattern S0 S1 S2 S3 S4 S5 S6 S7 S8 S9 分别为：1 X X X 0 1 X X 1 0。 然后我们将这 10 个方程写成矩阵形式，如下所示：  因此符合要求的该LFSR 的初始值是 “1” “1” “1” “0”. 注意：线性方程组并不总是可解的，在这种情况下，我们无法加载该特定pattern，因此将无法覆盖该pattern所针对的故障。变量的数量取决于 LFSR 的degree，更多的变量意味着获得解决方案的概率增加。 LFSR degree 假设我们有一个“N” degree的 LFSR，需要加载一个具有“S” bit的pattern，那么我们有“N”个变量和“S”个方程要求解。示例， 如果pattern为 1 X X X 0 1 X X 1 0，则“S”= 5。 现在，保证可以为给定pattern找到初始值所需的最小“N”是多少吗？ 研究表明，当 N ≥ (S+20) 时，找不到初始值的概率是 10-6（非常小）。 |
