|
一、半导体器件击穿原理 PN结I-V曲线如图[1]所示:PN结正向导通,反向截止;反向电压超过一定限值VBR,器件发生电击穿;正向导通时,电流超过一定限值(图示绿色区域之外),器件发生热烧毁。 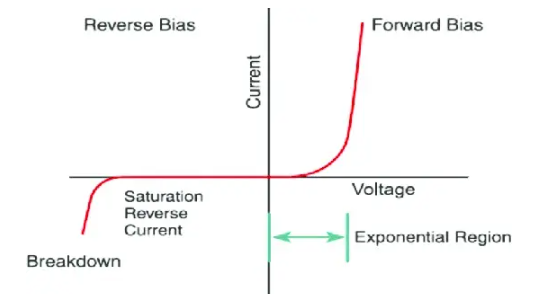 图[1]:PN结I-V曲线 PN结的击穿原理分为:电击穿和热击穿(二次击穿)。 1)电击穿 电击穿:指强电场导致器件的击穿,过程通常是可逆的。当电压消失,器件电学特性恢复。电击穿又分为: a)雪崩倍增效应 雪崩倍增效应:(通常指电压>6V时发生,)原理如下: 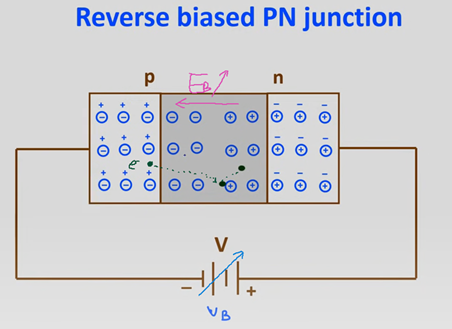 图[2]:PN结反偏示意图 如图[2]所示:在PN结两端加反向电压,随着反向电压增加,PN结耗尽区反向电场增加,耗尽区中电子(或者空穴)从电场中获得的能量增加。当电子(或者空穴)与晶格发生碰撞时传递给晶格的能量高于禁带宽度能量(Eg),迫使被碰撞的价带电子跃迁到导带,从而产生一堆新的电子空穴对,该过程叫做碰撞电离;课本里把一个自由电子(或者空穴)在单位距离内通过碰撞电离产生的新的电子空穴对的数目称为电子(或者空穴)的碰撞电离率,表示为αin(or αip)。 当耗尽区电场增加到一定程度,碰撞电离激发出的新电子-空穴对,即“二次载流子”,又可能继续产生新的载流子,这个过程将不断进行下去,称为雪崩倍增。如果由于雪崩倍增效应导致流出PN结的电流趋于无穷大,则发生了所谓的雪崩击穿,该过程简单示意如图[3]所示。  图[3]:雪崩击穿示意图 发生雪崩击穿的条件是: 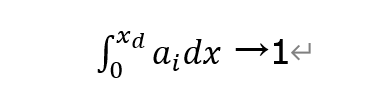 其物理意义是碰撞电离率在整个耗尽区积分趋于1。由于αi随电场的变化强相关(如图[4]所示),因此可以近似的认为当耗尽区最大电场EMAX达到某临界电场Ec时,即发生雪崩击穿。Ec与结的形式和掺杂浓度有一定关联,硅PN结典型值为Ec = 2×105 V/cm。 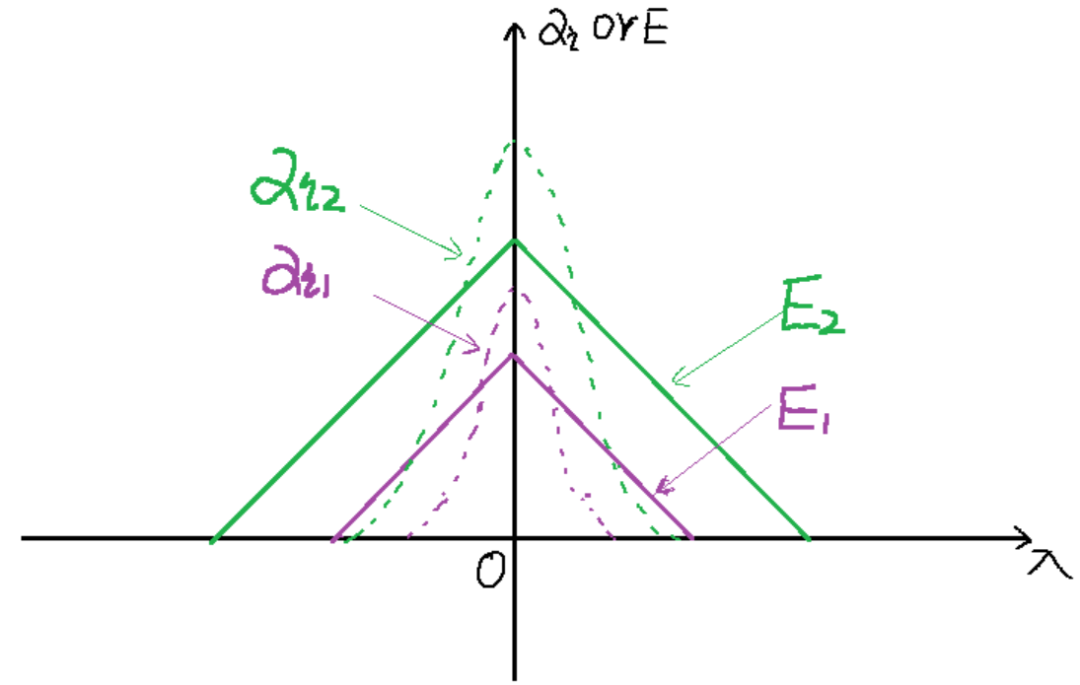 图[4]:电场的强相关函数图 为了更好地理解PN结电场强度Ec随耗尽区XD的关系,我们在这里简单讨论下泊松方程:在一维情况下(PN结/BJT)泊松方程的表达形式为:  等式右边第一项“q”为电荷量,介电常数“εs”为电通量密度与电场的映射关系,括号内表示自由离子的加和。从直观来看,该式反映电场(或者电通量密度,两者从某种角度上可以理解为反映着同一种东西)的源是电荷,如果是记公式:泊松方程表示的是,单位体积内对电通量密度(电位移)求散度,结果为体积内的电荷。除了从电磁学理论出发的分析,该式从数学上也可以看成是:电场与位置的函数关系。通过解泊松方程,便可以得到随着位置变化时,电场、电势的变化情况。 接下来我们通过举例来看击穿电压VB与哪些因素相关:图[5]所示为两种掺杂浓度材料的Ec VS Xd曲线关系(其中,N1>N2)。  图[5]不同掺杂浓度Ec VS Xd曲线关系 分析该图可知: 1. 禁带宽度Eg越大,则击穿电压VB越高;比如Si (Eg=1.12 eV) VS SiC (Eg=3.23 eV) 2. 掺杂浓度越低,VB越高; 3. 击穿电压主要取决于低掺杂一侧,该侧的杂质浓度越低,则VB越高。 除了上述方法可以提高击穿电压VB,还可以通过增加电场维度,改变电场强度分布(如图[6]、图[7]所示):比如英飞凌的CoolMOSTM系列产品,通过在N-耗尽区掺入P柱结构(引入横向电场分布),大幅提高VB。 |





