以下内容为可靠性知识共享学习会的会员朋友(匿名)的经验分享,非常感谢其支持与共享,谢谢!我们在设计试验确认可靠度是否达到目标要求时,产品在试验工况下的可靠度跟实际使用中该应力下的可靠度是什么关系呢?这里面牵扯到的东西非常多,今天这里考虑的情况比较单一,只是希望能给大家带来一点启示,并不追求全面而严谨。打个比方,我们的可靠性定量目标是,客户手中由于老化产生的累计失效概率为10年5%,而这些失效全部是一个机理,可以由高温加速,即 F(use,t=10年)=5% 那我们的样品在高温老化试验1000h下,可靠度是否也要求是95%呢? R(test,t=1000小时)=95%? 先看下这1000h是怎么来的。拿汽车举例,用户10年使用时间8000小时,提高温度算出加速系数是8,那试验时间就是8000/8=1000h。乍一看来,试验条件下,可靠度要求达到95%没毛病。但是,我们仔细琢磨下上面中的一句话,就会发现大有文章可做: “10年使用时间8000小时,温度加速系数是8”。 今天这里主要分析前半句,后半句是一样的道理,当然也可以扩展到其它更多的因素。 用户10年使用时间8000h,怎么来的呢?肯定不包括所有的用户,有些开黑车的老司机10年肯定远远不止这个数,有些就在家门口上班的小伙伴,可能10年才开了1000h。如果厂家工作到位的话,会对用户的使用情况做调查。当前我们正在走向万物互联的时代,用户调查也越来越好做,很多车厂都可以将用户的使用数据通过网络收集并分析。 假如我们发现用户的使用时间服从正态分布,u=8000h,σ=1000h f(t)=0.000398942EXP[-(t-8000)²/2000000] 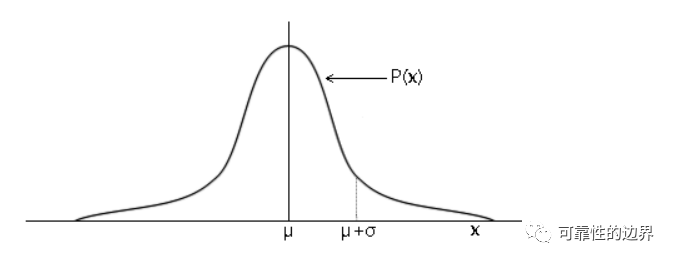 这里我们假设失效分布为指数分布,R(t)=EXP(-λt) R(8000h)=95%,则λ=-[ln(R(t))]/t=0.0000064117/h 结合用户分布,可靠度为多少呢,对f(t)R(t)在0到+∞进行积分 R=∫f(t)R(t)dt 下面,用excel进行简单的计算,这种方法并不精准,但是excel是我们每个人都有的软件,并且使用方法简单,不管用户分布和失效分布是什么样的,都可以这么算。 以1h为一个台阶进行积分,范围的话是±6σ,当然在实际计算的时候,可以根据自己的需要重新设定台阶和积分范围,台阶越小,积分范围越宽,算出来的也越准确。最后对f(t)d(t)列求和就可以了,如果台阶不是1,还要乘上台阶后求和。 如果8000h是包含了90%的用户呢,用户分布变了,计算方式还是一样的。 大家有时间可以分别计算一下这两种情况,看看算出来有什么不一样,差别还是挺大的。 如果没有一个合适的函数可以描述用户数据的分布,也没有关系,只要有用户数据,做出直方图,根据直方图每一数值对应的概率,也可以进行计算。 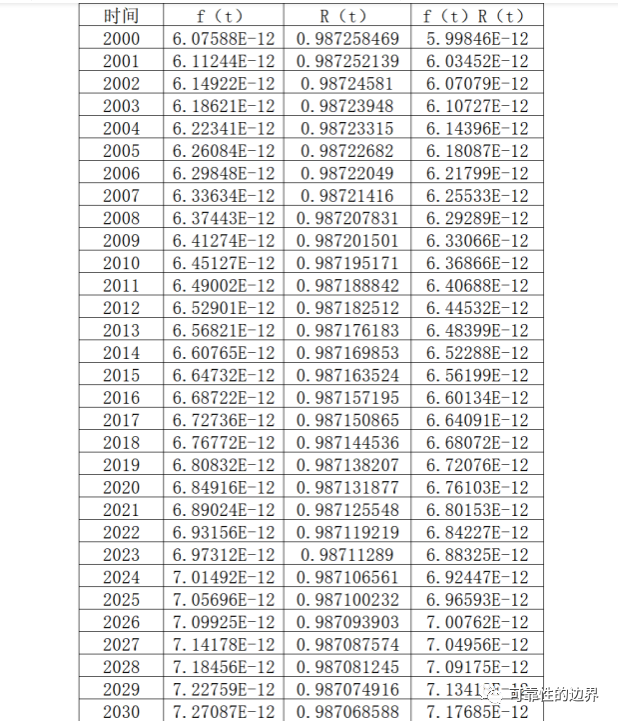 另外,使用excel,运用蒙特卡洛仿真的思想,也可以进行计算。首先生成用户分布的随机数,然后计算该数值下的可靠度。这种方法的话好处就是多个因素的话也可以进行方便的计算,缺点就是必须要有确定的分布函数才可以使用。 例如除了用户使用时间的分布,可以加上使用温度的分布,当初计算出的加速系数是8,是按照使用温度23℃,试验温度40℃来的。如果用户的使用温度也是按照某一特定分布来的,那也可以把温度的因素加进去。下面以温度分布为均值23℃,标准差5℃举例。 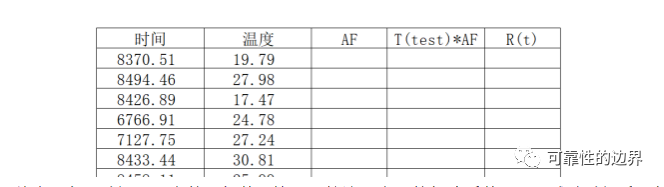 首先,生成时间和温度的随机数,然后计算该温度下的加速系数,再用试验时间乘以加速系数,则在该使用时间下可靠度为95%,就可以算出指数分布的失效率,进而可以得出第一列的时间,所对应的R(t)。至于随机数生成多少行,自己看着办吧,如果生成200行和1000行算出来的数差别很大,那肯定用1000行,如果1000行和10000行差别很小,那用1000行也行。 通过计算,我们发现,在试验工况下样品的可靠度是95%,对应到实际使用中的可靠性可能大,也可能小,差别也可能很大。GMW3172 handbook里面有说过这一点,当初看的时候还不是很理解,后来发现确实如此,相信很多小伙伴也没考虑过这一点。 |





