|
一、时域 时域是真实世界,是唯一实际存在的域。 当评估数字产品的性能时,通常在时域中进行分析。因为产品的性能最终要在时域中测量。 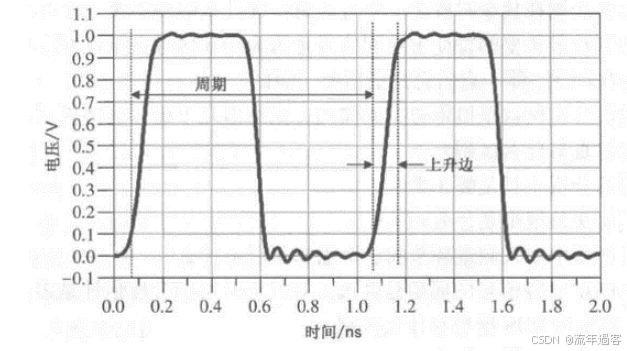 时钟波形的两个重要参数:时钟周期和上升沿, (1)时钟周期就是时钟循环重复一次的时间间隔,通常用ns(纳秒)度量。  (2)上升沿与信号从低电平跳变到高电平所经历的时间有关: 第一种定义是10%~90%(通常默认的表达方式); 第二种定义是20%~80%。 二、频域 频域最重要的性质是:它不是真实的,而是一个数学构造。 正弦波是频域中唯一存在的波形,这是频域中最重要的法则,即正弦波是频域的语言。(时域中的任何波形都可由正弦波的组合完全且唯一地描述) 频域中不可能产生新的信息。同一波形的时域或频域描述所包含的信息完全相同。 在频域中理解和描述一些问题要比在时域中更容易! 例如,带宽就是一个频域的概念,我们用它描述与信号、测量、模型或互连相关的最高有效正弦波频率分量。 1、正弦波 正弦波在时域中的描述,用以下3项可以充分描述正弦波:频率、幅度和相位,而在频域中只表示为一个点。 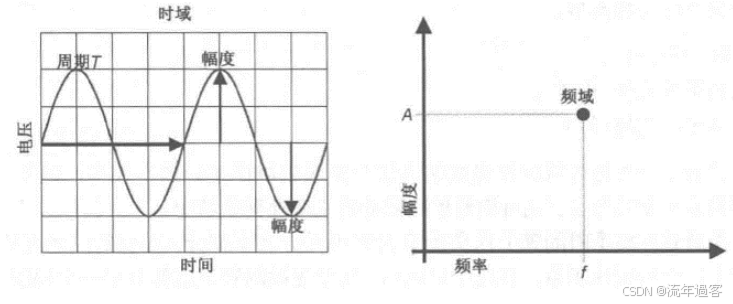 频率:通常用f来表示,指每秒中包含完整正弦波的周期数,单位是赫兹(Hz); 幅度:中间值之上最大的波峰高度值。水平轴之下和水平轴之上的波峰值相等。对于理想的正弦波,直流值或平均值始终为零; 相位:给出在时间轴起点的波的起始位置。相位以圆周、弧度(rad)或度(°)为单位。 2、时域与频域的转换–傅里叶变换 (1)傅里叶积分(FI) 傅里叶积分是一种将时域的理想数学表达变换成频域描述的数学技术。 例如,若时域中的整个波形只是一个短脉冲,就可用傅里叶积分将它变换到频域中。 傅里叶积分是在整个时间轴上从负无穷大到正无穷大求积分,得到的结果是零频率到正无穷大频率上连续的频域函数。在这个区间内,每个连续的频率点都对应一个幅值。 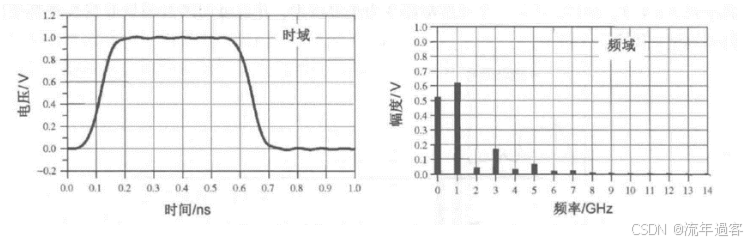 左图为1 GHz时钟信号在时域中的一个周期; 右图为在频域中的表示。 (2)离散傅里叶变换(DFT) 离散傅里叶变换是将波形变换到频域中。其中基本的假设就是原始的时域波形是周期的,它每隔T秒重复一次。与积分不同,此处只用到求和,通过简单的数学方法就能将任意一组数据变换到频域中。 (3)快速傅里叶变换(FFT) 除了计算每个频率点幅度值的实际算法使用了快速矩阵代数学的技巧,它与离散傅里叶变换是完全一样的。这种快速算法只应用于时域中的数据点个数是2的整幂次的情况,如256点、512点或1024点。根据所计算电压点个数的多少,快速傅里叶变换的计算速度比普通傅里叶变换可以快100~10000倍。 在频域中,对波形的描述变为不同频率正弦波的集合。每个频率分量都有对应的幅度及相位。所有这些频率点及其幅度值的全集称为波形的频谱。 3、重复信号的频谱 离散傅里叶变换或快速傅里叶变换是用于将实际波形从时域变换到频域的。对测量得到的任意波形,都能使用离散傅里叶变换,关键条件是该波形应是重复性,通常用大写字母F表示时域波形的重复频率。 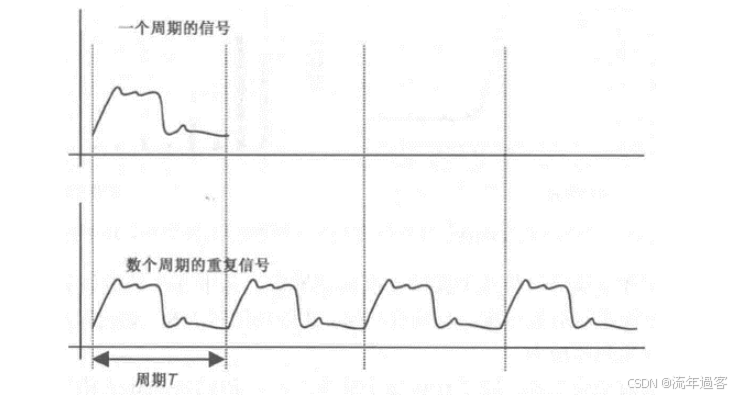 任何波形都可变成周期性的。 快速傅里叶变换只能对周期波形进行运算。 将波形的一段转换为重复波形时,可能会出现拼接不连续的现象。这种在接头处出现的非自然跳变,也会在离散傅里叶变换中产生拼接不连续现象。为了避免这个问题,通常采用加窗滤波器,以保证两头的电压在同一个值处连续。例如,汉明(Hamming)窗和汉宁(Hanning)窗就是实现这一功能的滤波器。 频谱中的正弦波频率应是重复频率的整倍数。若时钟频率为1GHz,离散傅里叶变换只有1GHz,2GHz,3GHz等正弦波分量。第一个正弦波频率称为1次谐波,第二个正弦波频率为2次谐波,以此类推。每个谐波都有不同的幅度和相位。所有谐波及其幅度的集合称为频谱。 4、理想方波的频谱 理想方波是对称的,其占空比是50%,并且峰值为1 V。 如果理想方波的重复频率为1GHz,其中频谱中的正弦波频率就是1GHz的整倍数。我们希望看到 f=1GHz,2GHz,3GHz等一些频率分量,但每个正弦波的幅度是多少呢? 所有偶次谐波(如2GHz,4GHz,6GHz)的幅度都为零,只有奇次谐波具有非零值。这是任何波形具备的特征,其波形的后半部分恰好是前半部分求反的结果。我们将这些波形称为反对称波形或奇对称波形。 奇次谐波的幅度An如下所示: An=2/(n π) n 为谐波次数(为奇数) 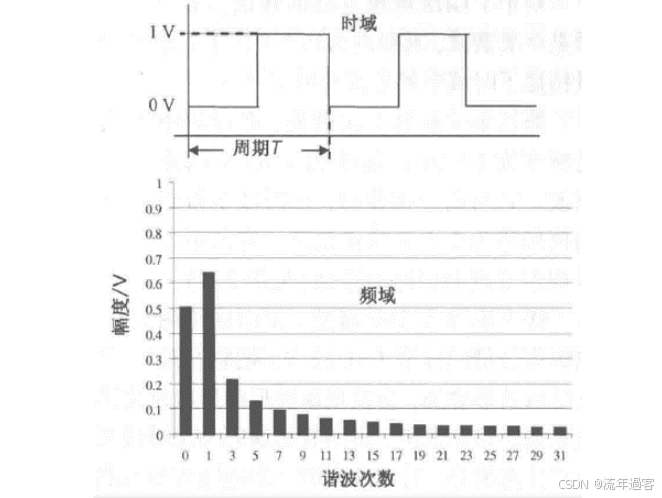 占空比为50%并从0 V跳变为1 V的理想方波,其1次谐波的幅度为0.63 V,3次谐波的幅度为0.21 V,1001次谐波的幅度为0.00063 V。要注意,当频率提高时,其幅度随着1/f 的减小而减小。 正弦波频率分量及其幅度的集合称为频谱,每一个分量称为谐波。 0次谐波就是直流分量值。 对于理想方波占空比为50%这一特殊情况,偶次谐波的幅度为零。任何谐波的幅度都可由2/(nπ) 计算得出。 三、从频域逆变到时域 在频域中,频谱表示时域波形包含的所有正弦波频率幅度。如果知道频谱,要想观察它的时域波形,则只需将每个频率分量逆变换成它的时域正弦波,再将其全部叠加即可。这个过程为傅里叶逆变换。 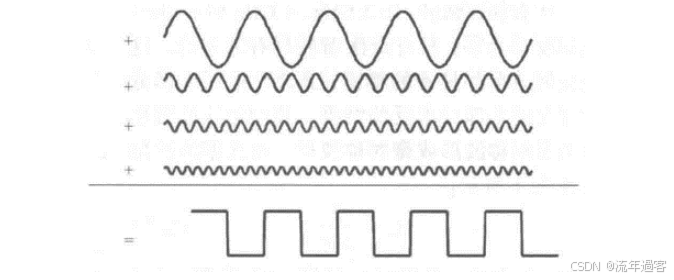 把以上每个正弦分量相叠加,即可将频谱转化为时域波形。 对于1GHz 理想方波的频谱,第一项是0次谐波,其幅度为0.5 V。这个分量描述了时域中的直流常量。 第二次分量是1次谐波,在时域中是频率为1 GHz且幅度为0.63 V的正弦波。它与前一项叠加,在时域中得到均值偏移为0.5 V的正弦波。它并不是对理想方波的很好的近似。 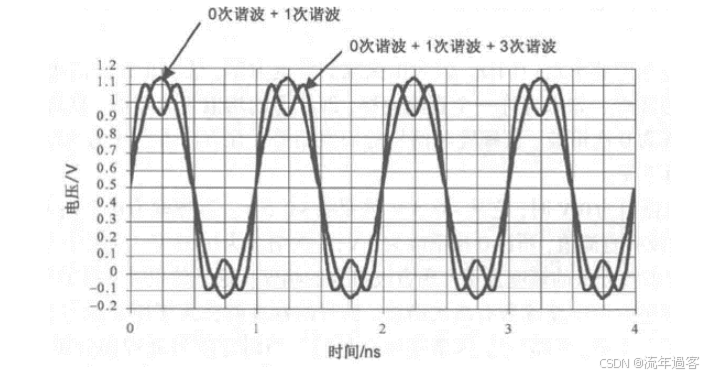 对于1 GHz理想方波,叠加0次谐波、1次谐波,接着加入3次谐波时形成的时域波形。 接下来加入3次谐波。3 GHz正弦波频率分量的幅度为0.21 V,把它与现有时域波形叠加,会发现新波形的形状发生了细微变化:顶端更平滑,更接近方波,且上升边更短。以此类推,将所有相继的高次谐波与已有波形相叠加,得出的结论越来越像方波。值得注意的是,时域波形的上升边随着加入高次谐波而变化。 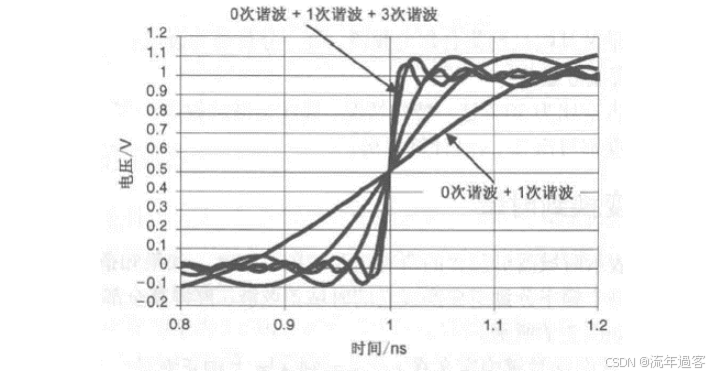 四、带宽对于上升沿的影响 带宽用于表示频谱中最高的有效正弦波频率分量值。带宽的选择对时域波形的最短上升边有直接的影响。对于数字信号,带宽同样指的是信号频谱中的频率范围。只不过对于数字信号而言,低频范围起始于直流分量并延伸到最高频率分量。在数字信号领域,因为最低频率是直流,所以带宽总是对应于最高的有效正弦波频率分量值。 一般而言,时域中上升边越短的波形在频域中的带宽就越高。如果改变频谱使波形的带宽降低,那么波形的上升边就会随之变长。 例1: 信号通过FR4板上4 in 长的传输线时,测量的正弦波频率分量衰减。在2 GHz以下频率分量的衰减不超过-1 dB,而10 GHz时的频率分量的衰减为-4 dB 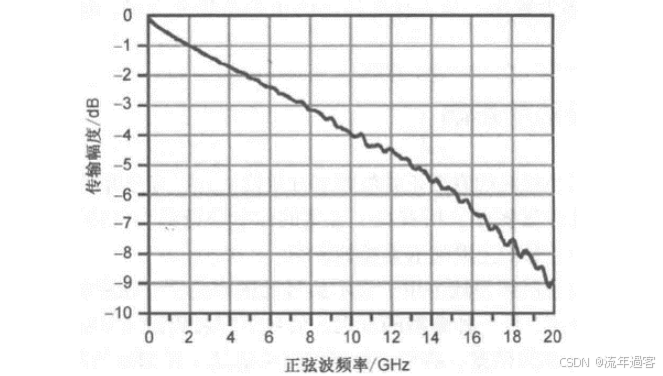 例2: 上升边为50 ps 的信号进入FR4 板上36 in 长的传输线时,以及离开传输线时的波形。由于高频分量的衰减比较多,其上升边从50 ps退化到1.5 ns。 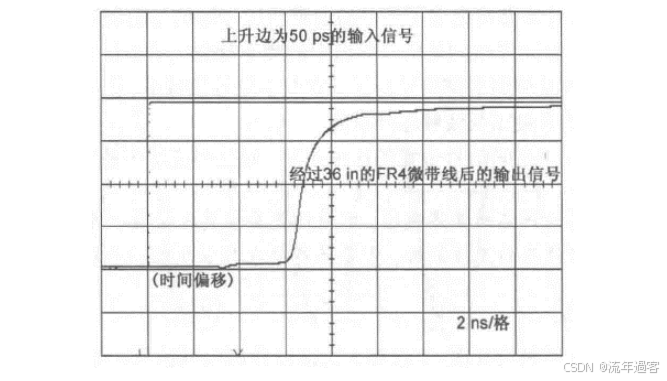 五、带宽与上升沿 因为每个波形都是通过加上某次谐波的正弦波频率分量而人为合成的,如果已知每个波形测量得到的10%~90%上升边和带宽,凭实验数据就能画出一个简单的关系。带宽与上升边的关系: 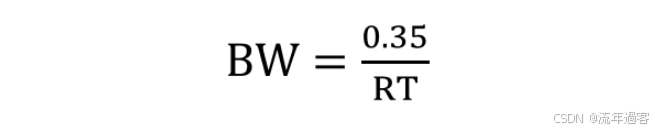 BW 表示带宽(单位为GHz) RT 表示10%~90%上升边(单位为ns) 例如: 当上升边的单位为ns时,带宽的单位为GHz。对于典型的10MHz的时钟信号,上升边一般为10 ns , 其带宽约为:0.35/10 ns =0.035 GHz,即35MHz。 信号的带宽定义为最高的有效正弦波频率分量。 如果把带宽内的所有频率分量都包含在内,就可以重新生成其上升边有限的方波,这时上升边与带宽的关系为: 上升边=0.35/BW 对于实际的时域波形,随着频率的升高,其频谱分量的幅度总是比理想方波中相同频率的幅度下降得快。有效性的问题其实就是一个频率点的问题,高于该点谐波分量的幅度比理想方波中相应频率分量的幅度要小; 所谓的“小”,通常指的是该分量的功率要小于理想方波中相应频率分量的功率的50%,功率下降50%也就是幅度下降至70%。这才是有效性的真正定义。若幅度高于理想方波中相同谐波幅度的70%以上,则称为有效。 从另一个稍微不同的角度看,可以把有效定义为实际波形的谐波分量开始比1/f下降得更快的那个频率点,该频率也称为转折频率。 对照方波的频谱,再看看梯形波的实际频谱,可以看出两者1次和3次谐波大致相同,梯形波的5次谐波约为方波的70%,依然占了很大的一部分。然而,梯形波的7次谐波只有理想方波的30%。 通过对梯形波谱的考察就可以得出结论: 高于5次谐波分量(如7次谐波或更高)的幅度 ,只相当于理想方波中电压总量的很小一部分。因此,它们对于上升边的影响也是微乎其微。与理想方波相比,从频谱中可以看梯形波中最高的有效正弦波分量为5次谐波,这是近似得出。 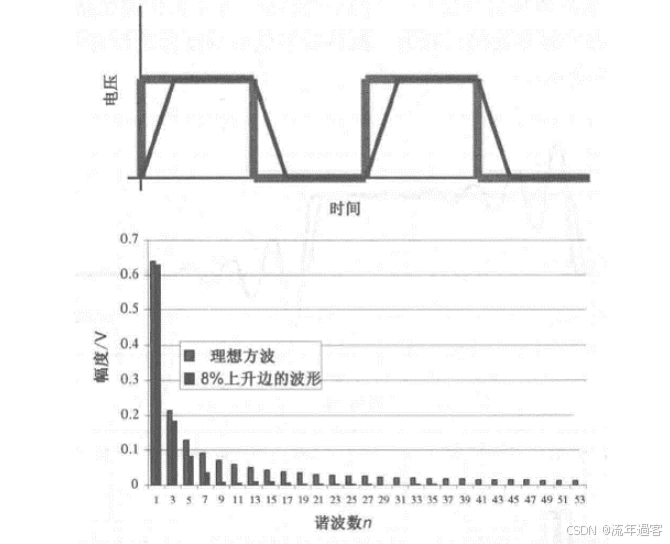 六、带宽 (1)实际信号的带宽 接近于理想方波的高质量信号都有一个简单的特征,即如果传输线路的端接欠佳,则信号会发生振铃,频谱在振铃频率处出现峰值。振铃频率处的幅度会比没 有振铃时的信号幅度高10倍以上。 电磁干扰由电流中每个频率分量的辐射引起。最严重的辐射源是共模电流,其总辐射将随着频率而线性增加。 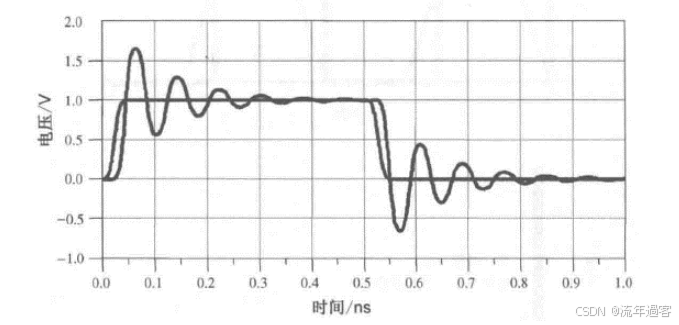 (2)时钟频率与带宽 带宽与信号的上升边直接有关。对于两个不同的波形,即使有相同的时钟频率,上升边和带宽也很可能不同。 下图4个不同的波形,每个波形都有1 GHz的相同时钟频率。各个信号是上升边不同,在周期中所占比例不同,因此它们的带宽也不同。需要注意的是,不是时钟频率而是上升边决定带宽。如果只知道波形的时钟频率,无法确定其带宽。 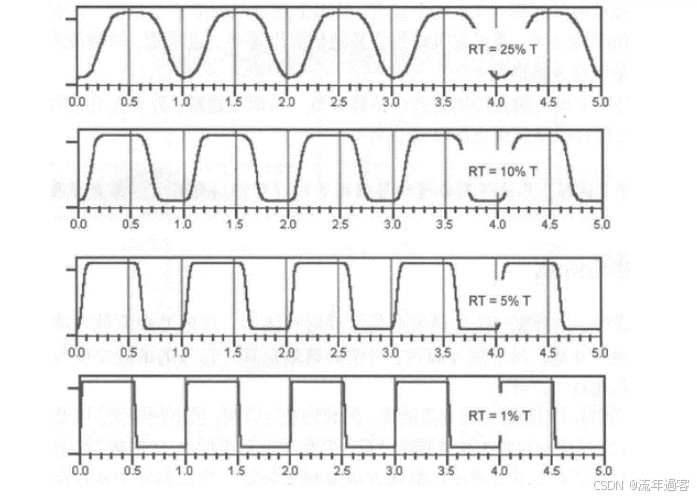 在实际的时钟波形中,上升边与时钟周期有什么关系?两者之间的唯一约束是:上升边一定小于周期的50%。 如果不知道上升边与周期的比值,则一个合理的概括是:上升边是时钟周期的7%。这与许多微处理器板和ASIC驱动板级总线的情况接近。  (3)测量的带宽 从1 MHz到1GHz测量去耦电容器的阻抗,可以看出在10MHz以下时,阻抗表现为理想电容器,但在10MHz以上时,它就表现为理想电感器。在矢量网络分析仪的整个测量范围内(此例中达到1GHz)。测量的带宽为1GHz。测量的带宽不同于元器件本身的可用带宽 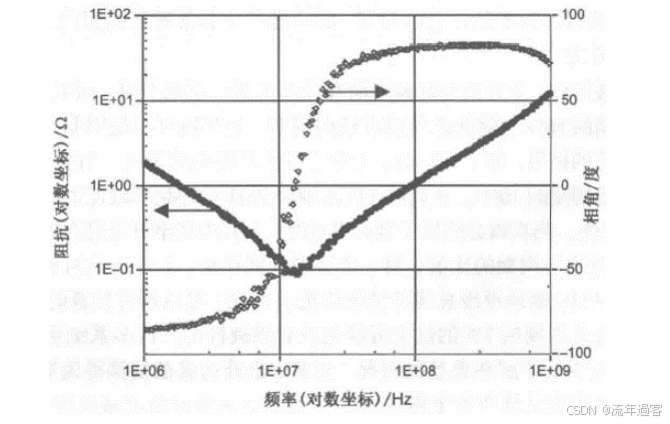 (4)模型的带宽 模型的带宽是指模型能被准确地用于预估实际结构真实性能的最高正弦波频率分量。 一个简单的初始电路模型由一个理想电感器和一个理想电阻器串联而成。2GHz之前,采用合适的L和R参数预估出的阻抗与实际测量的阻抗非常一致,所以这个简易模型的带宽就是2GHz。 超过2GHz采用带宽更高的模型,就能在更高频率上预估实际键合线的阻抗。这时就要考虑焊盘电容的影响,需要建立一个新模型,即二阶模型。 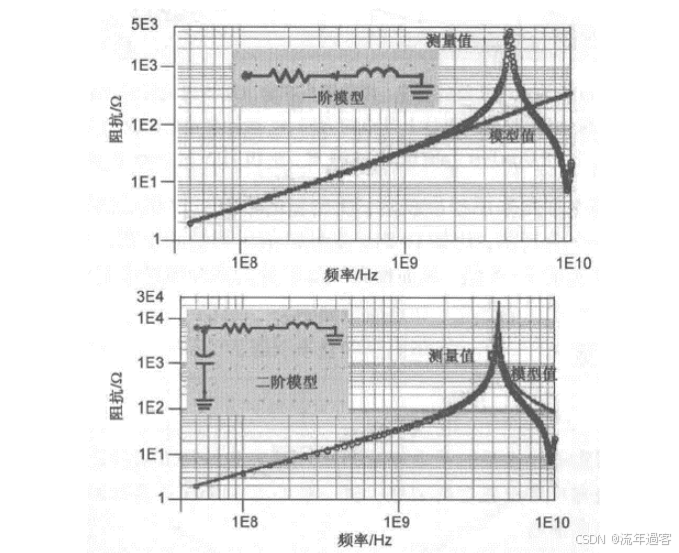 (5)互连的带宽 互连的带宽是指能被互连传输且未造成有限损耗的最高正弦波频率分量。 一般而言,在实际中使用的“有效”指的是传输的频率分量幅度减少了3 dB,也就是说幅度减少为入射值的70%。这就是经常提到的互连的3 dB带宽。 例如: 正弦波通过FR4板上的4 in 长的50 欧姆传输线后测量的幅度值, 这里的测量带宽为20 GHz。互连的3 dB带宽约为8 GHz,这意味着,如果输入一个8 GHz的正弦波,那么远端得到的信号幅度至多为原信号幅度的70%。如果互连的带宽为8 GHz,那么1 GHz的正弦波几乎100%传至互连的远端。 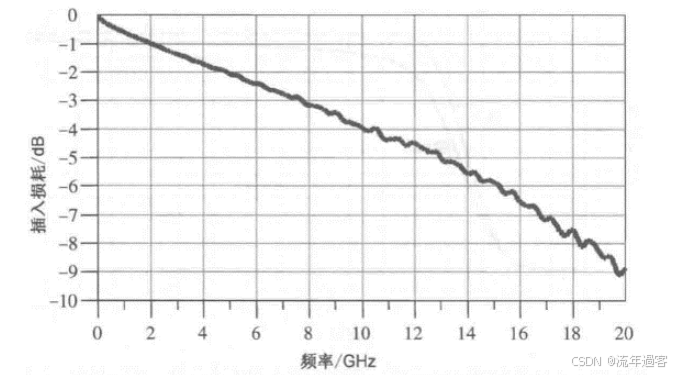 互连的带宽是对互连所能传输信号的最短上升边的直接度量。 一个上升边为1ps 的信号,在经过互连线传输后,其上升边可能为0.35/8 GHz=0.043 ns ,这说明互连使上升边退化了。如果互连的带宽是1GHz,所能传输信号的最快边沿就是350 ps,这就是互连的本征上升边。  例如: 经过FR4板上4 in长的50 Ω传输线,测得的输入和传输信号,可以看出,上升边发生了退化。 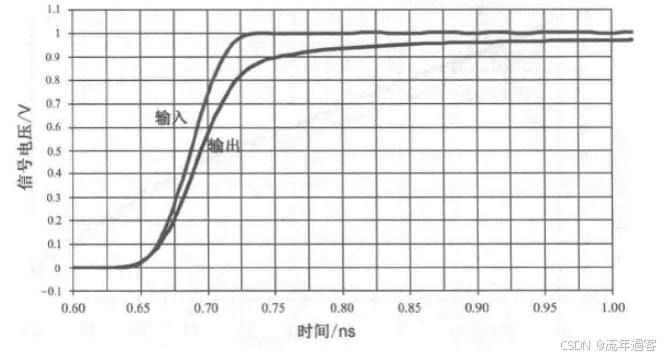 经验法则: 1.要使互连对信号上升边造成的附加量不超过10%,互连的本征上升边 就要小于该信号上升边的50%,这是个简单的经验法则。 2.从频率角度讲,为了较好地传输带宽为1GHz的信号,互连的带宽至少为该信号带宽的2倍,即2GHz。 (6)示波器的带宽 示波器的带宽是决定这台示波器测量最高频信号的能力 。 示波器的带宽主要是由前端的放大器等模拟器件的特性决定的 。 示波器中放大器的增益随着输入信号的频率升高而逐渐降低 。 放大器增益下降-3 dB对应的频点认为放大器的带宽,示波器的带宽也是这样定义的。 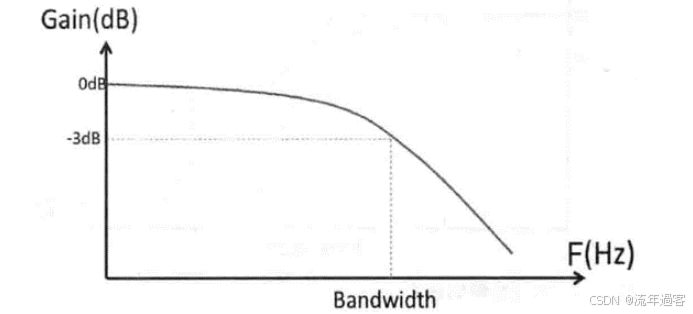 示波器的带宽可以理解为测量的幅度误差不超过-3 dB 的正弦波的频率值,超过这个频率值信号输入,就会衰减,示波器中再现的波形就失真过度了。 对数字信号来说,经验法则:示波器的带宽至少比被测系统最快的数字时钟速率高5倍。 |





