|
RC滤波电路 RC低通滤波器的基本结构如下图所示:  RC低通滤波器的基本结构 根据RC低通滤波器的频率响应曲线,其幅频曲线和相频曲线主要有如下特征: 1、上限频率f=1/(2πRC)。 上限频率之前的幅度变化接近于0dB,之后幅度按斜率-20dB/十倍频。 2、相位从0.1f处的0度滞后到10f处的90度滞后。 实际使用中具体选择R、C的值时,不仅要考虑R、C的频率特性,还要考虑信号源的内部阻抗和负载的阻抗: (1)C值的选取:C选的太小,导致负载电容对滤波电路的影响很大,一般IC的输入电容往往有1~10pF的输入电容。C值选的太大,则会影响滤波电路的高频特性,因为大电容的高频特性一般都不好。 (2)R值的选取:R值过小会加大电源的负载,R值过大则会消耗较多的能量。 RC滤波电路的最大缺陷就是它不仅消耗无用信号能量,而且也消耗有用信号能量。另外由于受电容高频特性的限制也不能用在频率较高的场合,例如数MHz以上需要用LC滤波器。 将R和C的位置互换可以得到RC高通滤波器,其频率响应与低通滤波器正好相反。 LC滤波电路 LC滤波电路应用较广泛,单板的电源滤波电路多采用LC滤波电路。LC滤波电路可以分成:L型、π型、T型、梯形。最简单的K型低通滤波器如下图所示:  简单的K型低通滤波器 L型滤波器的L和C的选取除了和RC滤波器一样要注意L和C的频率特性外,还需要注意阻抗匹配问题: 当终端阻抗比滤波器特性阻抗小时,Q值小于1,特性曲线呈圆弧状;终端阻抗比滤波器特性阻抗大时,特性曲线产生尖峰。 π型滤波器和T型滤波器有相同的衰减率,梯形滤波器为多个L型滤波器的串联,具有更高的衰减率。 无源LC滤波电路的灵敏度低,稳定性好。缺点是电感元件体积很大,成本较高,电感元件有时还需要磁屏蔽。 将电感和电容位置互换可以得到相应的高通滤波器。 有源模拟滤波器 如前所述,滤波器的设计最终需要物理实现,一般可以将复杂的高阶滤波器分解成一阶或者二阶的滤波器加以实现。在有源模拟滤波器是的设计中,运算放大器占有重要的位置,下面介绍一些由运放和无源器件构成的一阶和二阶有源滤波器: 1.一阶低通滤波器 在RC低通滤波器的输出端加一个电压跟随器,即可以构成一个简单的一阶有源低通滤波器。如下图所示:  简单的一阶有源低通滤波器 如上图所示,有:  电路的传递函数直接可得:  式中ωp=1/RC,称为特征角频率。由于传递函数的分母为S的一次幂,称为一阶有源低通滤波器。其幅频特性和相频特性如下图所示: 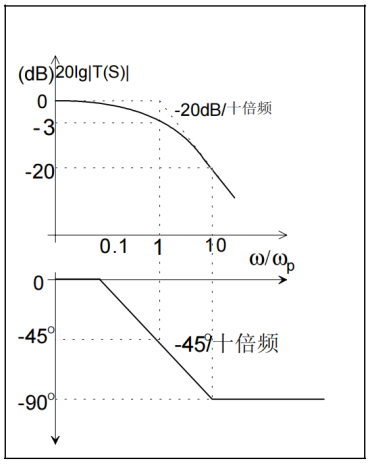 一阶低通滤波器的幅频特性和相频特性 可以看到,其响应特性与RC无源低通滤波器一样,只是增加了带负载的能力。 2.二阶有源低通滤波器 上面的一阶低通滤波器的衰减斜率为-20dB/十倍频,选择性较差。采用如下图的电路则可以得到改进:  二阶低通滤波器 电路的传递函数为二阶的:  通带截止频率为ωp=0.37/(RC),幅频特性的斜率为-40dB/十倍频。 3.Butterworth低通滤波器 巴特沃斯滤波器的幅频特性是单调的,且在通带内比较平坦。高阶巴特沃斯滤波器的幅频特性仍然是单调的,且在通带内更为平坦。其幅频特性一般可表示为:  其幅频特性如下图所示:  巴特沃斯滤波器的幅频特性 4.Chebyshev滤波器 切比雪夫型滤波器的幅频通带范围内有起伏,但在ω>ωp且接近ωp时下降较陡。其幅频特性一般可表示为:  其幅频特性如下图所示:  Chebyshev滤波器的幅频特性 5.Bessel滤波器 贝塞尔滤波器的特点是相频特性在一段频率范围内线性度较好,且相移比巴特沃斯或切比雪夫的相移小,同时其阶跃响应没有过程现象。 6.椭圆滤波器 椭圆滤波器由于在阻带内有衰减极点,幅频特性在过渡带内下降比上三种滤波器都快。椭圆滤波器在通带内也有波动。 实际应用中需要根据侧重点的不同选用合适的滤波方式。 |





