|
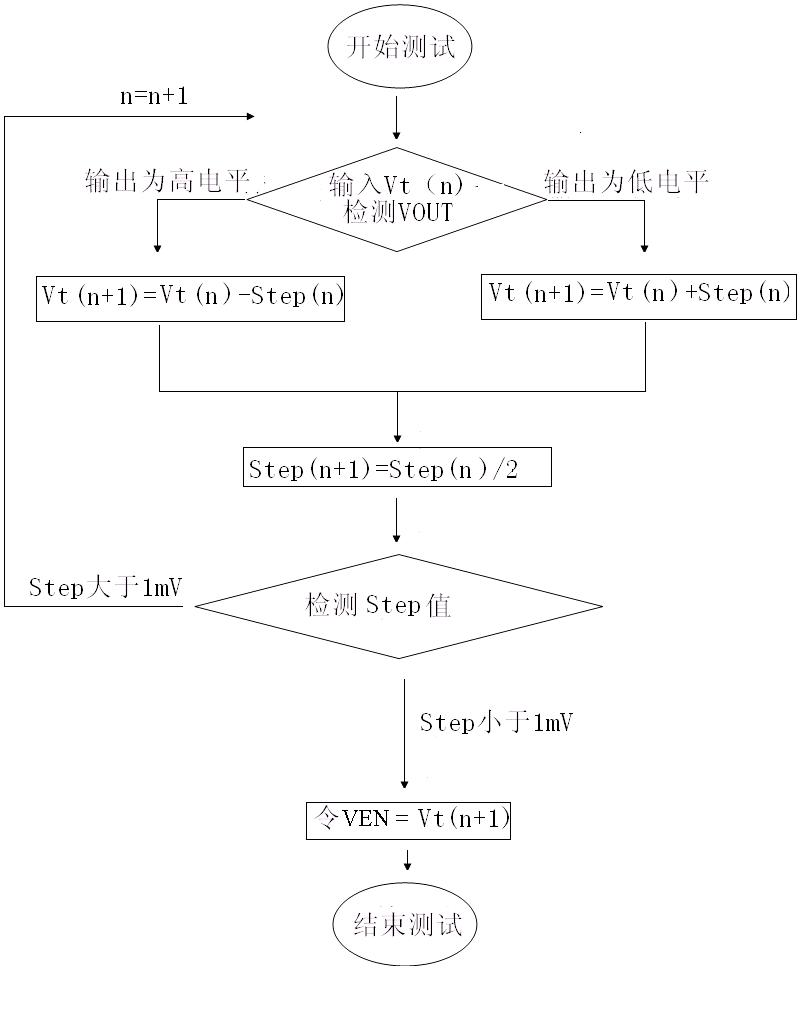
测试中经常有些参数要用扫描方式实现,如阈值电压的测试。本文将以测试阈值电压为例,介绍如何用二分法来进行扫描测试。 一般常用的扫描测试方法,是逐点扫描,即在一定的范围内逐点增/减电压,每次调整需延迟一段时间,待芯片稳定再根据输出结果来判定阈值。 如图1示是一个Reset电路原理框图,我们来分析一下其VTH测试,假设输入电压检测范围为0.5V,测试精度要求为正负1mV。 使用逐点加压测试的方法,假设每次改变输入电压后芯片稳定及测量的总时间平均为2mS,取电压点间隔=1mV*2,则最大测试时间=0.5V/2mV*2mS=500mS。一般情况下,假设实际值在扫描范围的中间位置,取平均测试时间=500mS/2=250mS。 然而250mS的扫描时间,在实际量产时是无法接受的。我们做另外一种假设,如果要求测试时间缩短均为15mS以内。 仍然用逐点加压测试的方法,每次改变输入电压后,芯片稳定及测量的总时间平均为2mS,则测试点数量=15mS/2mS=7.5,取8,误差=0.5V/8/2=31.25mV。 由上面的计算可见,因为测试机输出电压、芯片稳定、检测电压都要消耗一定的时间。所以使用这 种测试方法,会存在测试精度与测试效率之间的矛盾。如果使检测点很密以提高精度,则非常耗时;如果要减少测试时间,提高效率,则必须加大检测点之间的间 隔,那么相应的就会造成测试精度的降低。 而测试时间是测试方案优劣的一个测试重要考量。逐点加压测试耗时严重,且精度不高。考虑是否可以从单纯的软件优化的角度来达到测试精度与测试效率之间的矛盾的平衡。 下面介绍如何使用二分法测试来同时提高测试精度与测试效率。二分法是通过动态增/减电压,减少测试点方式来提高效率,并同时通过逐次逼近的方式缩小待测范围,保证精度,实现了测试精度与测试效率之间的一种平衡。 如图2示,中间的长细线表示当前的测试扫描点,红色圆点是实际的电路阈值电压点,固定不动的两根较粗的线是初始上下限值,绿色的点线是当前的上限值,黄色的连续线是当前的下限值。由高点开始检测的二分法简化为4个步骤讨论,如下, 步骤1,以1/2上下限值为起始扫描点,通过第一次扫描可知实际阈值电压点在扫描点之下; 步骤2,调整上限扫描点至步骤1的扫描点,可知阈值电压点在扫描点之上; 步骤3,调整下限扫描点至步骤2扫描点,可知阈值电压点在扫描点之下; 步骤4,不断重复步骤2与步骤3,直到上下限之差达到测试精度要求,则停止扫描。 最终扫描点上下限平均值就是所求的阈值点。为了保证测试值正确,可以将所得的阈值点加减一定电压进行验证。 由上面的演示可以知道,二分法的上下限是以2的指数形式迅速改变的,以0.5V范围为例,在8次测试之后,上下限间隔只有0.5V/256=2mV左右,误差在1mV之内,可见二分法测试确实是一种高效高精度的扫描测试方法。 二分法编程实现流程原理如图3示。 需要注意的是,当阈值电压存在迟滞效应时,不适合套用上述方法,二分法测试的流程还需要优化,此处暂不赘述。 下面以一个带使能端的LDO为例介绍这种算法。其典型应用电路如图1示,当EN引脚输入为高,OUT引脚输出高电平;当EN引脚输入为低,OUT截止,输出低电平。 算法实现过程如下: 假设:待测参数VEN的上下限为1.3V~1.6V,测试精度要求为1mV,且没有迟滞效应。 步骤一:定义变量Vt,初始值为二分之一上下限,即(1.3+1.6)/2=1.45V;定义变量Step,初始值建议设定为四分之一的公差,即(1.6-1.3)/4=0.075V。 步骤二:在EN引脚加电压Vt,检测VOUT输出,若OUT引脚输出为低电平,则令 Vt(n+1)=Vt(n)+Step(n);若OUT引脚输出为高电平,则令 Vt(n+1)=Vt(n)-Step(n)。并令Step(n+1)= Step(n)/2。 步骤三:循环执行步骤二。当Step达到精度要求时,停止循环。此时的Vt即是待测值VEN。其编程原理流程图如图2示。 测试结束后,可以通过对VEN加上或减去一个小电压,再将其加到EN引脚上,观察OUT输出是否符合预期,来达到检测测试结果是否准确的目的。
另外只要对算法稍作改进,二分法也是可以用于测试存在迟滞效应的阈值信号。具体方法是,每次在步骤二开始时,对EN进行复位,加上一个电压V0:测试VIH,则设置V0为低电平;测试VIL,则设置V0为高电平。
|